题目内容
已知△ABC中，AB=
，BC=8，BC边上的中线，AD=3，求△ABC的面积．
| 7 |
考点：勾股定理
专题：计算题
分析：由BC的长，D为BC中点，求出BD的长，在三角形ABD中，利用勾股定理的逆定理得到三角形ABD为直角三角形，BD为斜边，求出三角形ABD面积，利用等底同高三角形面积相等即可确定出三角形ABC面积．
解答：解：∵BC=8，D为BC的中点，
∴BD=CD=4，
在△ABD中，AB=
，AD=3，BD=4，
∴AB2+AD2=BD2，
∴S△ABD=
AD•AB=
，
则S△ABC=2S△ABD=3
．
∴BD=CD=4，
在△ABD中，AB=
| 7 |
∴AB2+AD2=BD2，
∴S△ABD=
| 1 |
| 2 |
3
| ||
| 2 |
则S△ABC=2S△ABD=3
| 7 |
点评：此题考查了勾股定理，以及三角形的面积，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
如图，在小正方形组成的网格中，图②是由图①经过旋转变换得到的，其旋转中心是点
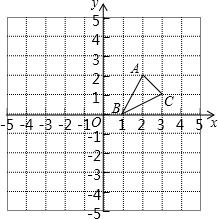如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，三个顶点的坐标分别为A（2，2），B（1，0），C（3，1）
如图，直线AB、CD相交于O点，若∠COE=∠FOB=90°，∠AOC=30°，则∠EOF=