题目内容
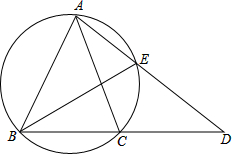 如图,已知E是等腰△ABC外接圆上的点,
如图,已知E是等腰△ABC外接圆上的点, |
| AE |
 |
| CE |
考点:圆周角定理,等腰三角形的判定与性质,圆心角、弧、弦的关系
专题:证明题
分析:由条件可知∠CBE=∠CAE=∠ABE,由外角性质可知∠ACB=∠CAD+∠D=∠ABC,可得∠EBD=∠D,可证明DE=BE.
解答:证明:
∵
=
,
∴∠ABE=∠EBD=∠EAC,
∵∠ACB=∠EAC+∠D,
∴∠ACB=∠EBD+∠D,
∵AB=AC,
∴∠ABC=∠ACB=∠ABE+∠EBD,
∴∠EAC+∠EBD=∠EBD+∠D,
∴∠EBC=∠D,
∴DE=BE.
∵
 |
| AE |
 |
| CE |
∴∠ABE=∠EBD=∠EAC,
∵∠ACB=∠EAC+∠D,
∴∠ACB=∠EBD+∠D,
∵AB=AC,
∴∠ABC=∠ACB=∠ABE+∠EBD,
∴∠EAC+∠EBD=∠EBD+∠D,
∴∠EBC=∠D,
∴DE=BE.
点评:本题主要考查圆周角定理及等腰三角形的性质和判定,掌握在同圆中同弧或等弧所对的圆周角相等是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
如图,函数y1=ax+b与y2=bx+a正确的图象为( )
A、 |
B、 |
C、 |
D、 |
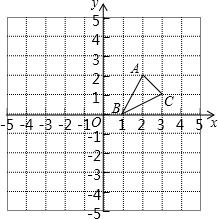 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1) 如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E.已知GB=10cm,AG=2cm,DE=3cm,求EF的长.
如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E.已知GB=10cm,AG=2cm,DE=3cm,求EF的长. 如图,
如图,