题目内容
已知a1=1-m,a2=1-
,a3=1-
…,第n个数是 .
| 1 |
| a1 |
| 1 |
| a2 |
考点:规律型:数字的变化类
专题:
分析:先用含m的式子表示a1=1-m,a2=1-
=
,a3=1-
=
,a4=1-
=1-m,…,然后寻求规律3个一循环,然后分三种情况:①第n个数是3的倍数,答案为
;②第n个数是3的倍数余1,答案为1-m;③第n个数是3的倍数余2,答案为
.
| 1 |
| a1 |
| m |
| m-1 |
| 1 |
| a2 |
| 1 |
| m |
| 1 |
| a3 |
| 1 |
| m |
| m |
| m-1 |
解答:解:∵a1=1-m,
∴a2=1-
=
,
a3=1-
=
,
a4=1-
=1-m,…,
3个一循环,
分三种情况:
①当第n个数是3的倍数时,
an=a3=
;
②当第n个数是3的倍数余1时,
an=a1=1-m;
③当第n个数是3的倍数余2时,an=a2=
.
故答案为:
或1-m或
.
∴a2=1-
| 1 |
| a1 |
| m |
| m-1 |
a3=1-
| 1 |
| a2 |
| 1 |
| m |
a4=1-
| 1 |
| a3 |
3个一循环,
分三种情况:
①当第n个数是3的倍数时,
an=a3=
| 1 |
| m |
②当第n个数是3的倍数余1时,
an=a1=1-m;
③当第n个数是3的倍数余2时,an=a2=
| m |
| m-1 |
故答案为:
| 1 |
| m |
| m |
| m-1 |
点评:此题考查了有数字的变化寻找规律,解题的关键是:先用含m的式子表示a1、a2、a3、a4,…,然后寻找规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
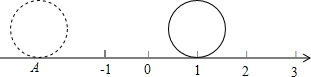 如图所示,直径为单位1的圆从数轴上表示1的点沿着数轴无滑动地逆时针滚动一周到达A点,则A点表示的数是( )
如图所示,直径为单位1的圆从数轴上表示1的点沿着数轴无滑动地逆时针滚动一周到达A点,则A点表示的数是( )| A、-π+1 | B、-π-1 |
| C、π+1 | D、π-1 |
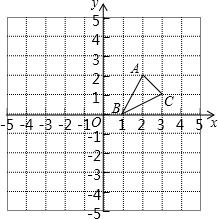 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1) 如图,
如图,
 如图,直线AB、CD相交于O点,若∠COE=∠FOB=90°,∠AOC=30°,则∠EOF=
如图,直线AB、CD相交于O点,若∠COE=∠FOB=90°,∠AOC=30°,则∠EOF=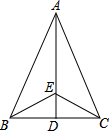 如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,若点E是AD上的任意一点,连接BE、CE,试探求∠EBD与∠ECD的大小关系,并说明理由.
如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,若点E是AD上的任意一点,连接BE、CE,试探求∠EBD与∠ECD的大小关系,并说明理由.