题目内容
已知等腰△ABC的周长为2+
,腰AB的长为1,求其底角度数.
| 2 |
考点:解直角三角形,等腰三角形的性质
专题:
分析:根据等腰△ABC的腰AB的长为1,周长为2+
,可求得BC的长,根据勾股定理的逆定理即可求得该三角形为等腰直角三角形,即可求得底角度数.
| 2 |
解答:解:∵等腰△ABC的腰AB的长为1,周长为2+
,
∴AB=AC=1,
∴底边长BC=2+
-1-1=
.
∵AB2+AC2=BC2,
∴△ABC为直角三角形,
∵△ABC是等腰三角形,
∴△ABC是等腰直角三角形.
∴底角为45°.
| 2 |
∴AB=AC=1,
∴底边长BC=2+
| 2 |
| 2 |
∵AB2+AC2=BC2,
∴△ABC为直角三角形,
∵△ABC是等腰三角形,
∴△ABC是等腰直角三角形.
∴底角为45°.
点评:本题考查了勾股定理逆定理的运用,考查了等腰直角三角形底角为45°的性质,本题中求证△ABC是直角三角形是解题的关键.

练习册系列答案
相关题目
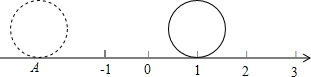 如图所示,直径为单位1的圆从数轴上表示1的点沿着数轴无滑动地逆时针滚动一周到达A点,则A点表示的数是( )
如图所示,直径为单位1的圆从数轴上表示1的点沿着数轴无滑动地逆时针滚动一周到达A点,则A点表示的数是( )| A、-π+1 | B、-π-1 |
| C、π+1 | D、π-1 |
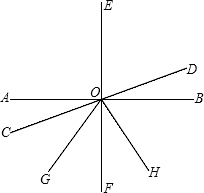 如图,AB、CD、EF相交于点O,EF⊥AB,OG、OH分别为∠COF、∠DOG的平分线,若∠AOC:∠COG=4:7,则∠DOF=
如图,AB、CD、EF相交于点O,EF⊥AB,OG、OH分别为∠COF、∠DOG的平分线,若∠AOC:∠COG=4:7,则∠DOF=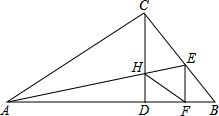 如图,在Rt△ABC中,∠ACB=90°,过C作AB的垂线CD交AB于D,过A作∠BAC的角平分线AE交BC于E,AE交CO于H,过E作EF⊥AB交AB于F,连接HF,求证:四边形CHFE为菱形.
如图,在Rt△ABC中,∠ACB=90°,过C作AB的垂线CD交AB于D,过A作∠BAC的角平分线AE交BC于E,AE交CO于H,过E作EF⊥AB交AB于F,连接HF,求证:四边形CHFE为菱形.