题目内容
4.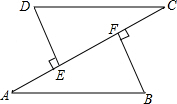 已知:如图,AE=CF,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF.求证:AB∥CD.
已知:如图,AE=CF,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF.求证:AB∥CD.
分析 要证AB∥CD,可通过证∠A=∠C,那么就需证明这两个角所在的三角形全等即可.
解答 解:如图,∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°.
又∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在△AFB与△CED中,
$\left\{\begin{array}{l}{BF=DE}\\{∠BFA=∠DEC}\\{AF=CE}\end{array}\right.$,
∴△AFB≌△CED(SAS).
∴∠A=∠C.
∴AB∥CD.
点评 本题考查了三角形全等的判定及性质;题目采用从结论开始推理容易突破.有平行推出需要找到有关角相等,进而分析需证三角形全等.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
13.在直角坐标系中,O为坐标原点,已知A(2,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=4,则CD的长为8.
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=4,则CD的长为8.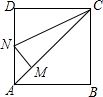 如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°.
如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°. 如图,∠1=130°,∠2=130°,∠3=120°,试确定∠4的度数.
如图,∠1=130°,∠2=130°,∠3=120°,试确定∠4的度数.