题目内容
17.(1)计算:($\sqrt{3}$+1)2-6$\sqrt{\frac{1}{3}}$;(2)解方程组:$\left\{\begin{array}{l}{x+2y=5①}\\{3x-2y=-1②}\end{array}\right.$.
分析 (1)先利用完全平方公式计算,然后把二次根式化为最简二次根式后合并即可;
(2)利用加减消元法解方程组.
解答 解:(1)原式=3+2$\sqrt{3}$+1-2$\sqrt{3}$
=4;
(2)①+②得4x=5,解得x=1,
把x=1代入①得1+2y=5,解得y=2,
所以方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解二元一次方程组.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
8.若点A(2,3)在反比例函数y=$\frac{k}{x}$的图象上,则该图象一定经过点( )
| A. | (-2,3) | B. | (1,-6) | C. | (-3,-2) | D. | (3,3) |
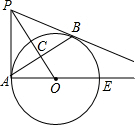 如图,已知点P是⊙O外一点,PB切⊙O于点B,BA 垂直OP于C,交⊙O于点A,连接PA、AO,延长AO,交⊙O于点E.
如图,已知点P是⊙O外一点,PB切⊙O于点B,BA 垂直OP于C,交⊙O于点A,连接PA、AO,延长AO,交⊙O于点E. 如图,在⊙O的内接五边形ABCDE中,∠B+∠E=215°,则∠CAD=35°.
如图,在⊙O的内接五边形ABCDE中,∠B+∠E=215°,则∠CAD=35°. 如图,平面直角坐标系xOy中,点A是直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$上一动点,将点A向右平移1个单位得到点B,点C(1,0),则OB+CB的最小值为$\sqrt{13}$.
如图,平面直角坐标系xOy中,点A是直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$上一动点,将点A向右平移1个单位得到点B,点C(1,0),则OB+CB的最小值为$\sqrt{13}$.