题目内容
2.已知关于x的一元二次方程x2+4x+m-1=0.(1)当m何值时,方程有两个相等的实数根;
(2)当m=2时,设α、β是方程的两个实数根,求α2+β2+αβ的值.
分析 (1)根据根的判别式△=0解答;
(2)利用根与系数的关系的关系解答.
解答 解:(1)依题意得:△=42-4(m-1)=0,
解得m=5;
(2)∵当m=2时,设α、β是方程的两个实数根,
∴α+β=-4,αβ=m-1=1,
∴α2+β2+αβ=(α+β)2-αβ=(-4)2-1=15,
即α2+β2+αβ=15.
点评 本题考查了根与系数的关系,根的判别式.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
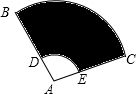 如图,扇形纸扇完全打开后,外侧两竹条AB、AC夹角为120°,AB的长为30cm,无贴纸部分AD的长为10cm,则贴纸部分的面积等于$\frac{800}{3}$πcm2.
如图,扇形纸扇完全打开后,外侧两竹条AB、AC夹角为120°,AB的长为30cm,无贴纸部分AD的长为10cm,则贴纸部分的面积等于$\frac{800}{3}$πcm2.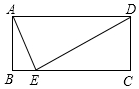 如图,在矩形ABCD中,点E在BC上,连接AE、DE,若AD=DE=2,∠BAE=15°,则CE的长为$\sqrt{3}$.
如图,在矩形ABCD中,点E在BC上,连接AE、DE,若AD=DE=2,∠BAE=15°,则CE的长为$\sqrt{3}$.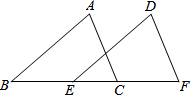 如图,点B、E、C、F在同一条直线上,AC=DF,AB∥DE,∠A=∠D,求证:BE=CF.
如图,点B、E、C、F在同一条直线上,AC=DF,AB∥DE,∠A=∠D,求证:BE=CF.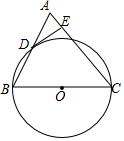 如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.
如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.