题目内容
8.如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径总长度为( )
| A. | $\frac{16\sqrt{3}π}{3}$ | B. | $\frac{16π}{3}$ | C. | $\frac{4π}{3}+\frac{4\sqrt{3}π}{3}$ | D. | $\frac{8π}{3}+\frac{8\sqrt{3}π}{3}$ |
分析 画出图形即可知道,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为图中的弧线长,由此即可解决问题.
解答 解:如图,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为图中弧线长.
由题意可知$\widehat{AD}$=$\widehat{{A}_{2}{A}_{3}}$,∠DOA2=120°,DO=4$\sqrt{3}$,
所以点A运动经过的路径的长度=2×$\frac{60π×4}{180}$+$\frac{120π×4\sqrt{3}}{180}$=$\frac{8}{3}$π+$\frac{8}{3}\sqrt{3}$π,
故选:D.
点评 本题考查菱形的性质、弧长公式等知识,解题的关键是正确画出图象,探究点A的运动轨迹,解题时注意正确运用弧长公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R).

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
19.一个猜想是否正确,科学家们要经过反复的论证.表是几位科学家“掷硬币”的实验数据:
请根据以上数据,估计硬币出现“正面朝上”的概率为0.50(精确到0.01).
| 实验者 | 德•摩根 | 蒲丰 | 费勒 | 皮尔逊 | 罗曼诺夫斯基 |
| 掷币次数 | 6 140 | 4 040 | 10 000 | 36 000 | 80 640 |
| 出现“正面朝上”的次数 | 3 109 | 2 048 | 4 979 | 18 031 | 39 699 |
| 频率 | 0.506 | 0.507 | 0.498 | 0.501 | 0.492 |
16.若一组数据2,4,6,8,x的方差比另一组数据5,7,9,11,13的方差大,则 x 的值可以为( )
| A. | 12 | B. | 10 | C. | 2 | D. | 0 |
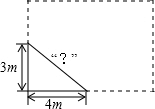 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.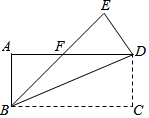 如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.
如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.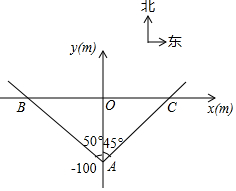 某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即$\frac{50}{3}$m/s),交通管理部门在离该公路100m处设置了一速度监测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西50°方向上,点C在点A的北偏东45°方向上.
某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即$\frac{50}{3}$m/s),交通管理部门在离该公路100m处设置了一速度监测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西50°方向上,点C在点A的北偏东45°方向上.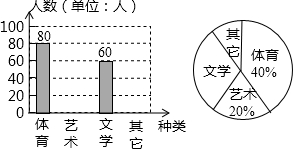 为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题: 请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为$\sqrt{2}$,$\sqrt{10}$,4$\sqrt{\frac{1}{2}}$.
请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为$\sqrt{2}$,$\sqrt{10}$,4$\sqrt{\frac{1}{2}}$.