题目内容
7.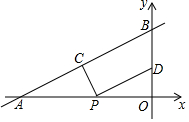 如图,在平面直角坐标系中,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,若点P为OA上一动点,则PC+PD值最小时OP的长为( )
如图,在平面直角坐标系中,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,若点P为OA上一动点,则PC+PD值最小时OP的长为( )| A. | 3 | B. | 6 | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
分析 作点C关于x轴的对称点C′,连接CC′交x轴于点E,连接C′D交x轴于点P′,此时P′C+P′D值最小,过点C′作CF⊥y轴于点F,利用三角形中位线可求出点C、D的坐标,由对称可求出点C′、F的坐标,再利用三角形的中位线可求出OP′的值,此题得解.
解答 解:作点C关于x轴的对称点C′,连接CC′交x轴于点E,连接C′D交x轴于点P′,此时P′C+P′D值最小,过点C′作CF⊥y轴于点F,如图所示.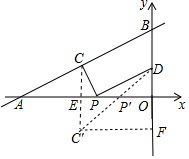
∵直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,
∴点A(-6,0),点B(0,4).
∵AE∥BO,点C为AB的中点,
∴CE为△ABO的中位线,
∴OE=$\frac{1}{2}$OA,CE=$\frac{1}{2}$OB,
∴点C(-3,2).
同理可得出点D(0,2).
∵点C、C′关于x轴对称,
∴点C′(-3,-2),F(0,-2),
∴点O为DF的中点,
∴OP′为△DC′F的中位线,
∴OP′=$\frac{1}{2}$C′F=$\frac{3}{2}$.
故选D.
点评 本题考查了一次函数图象上点的坐标特征、三角形的中位线以及轴对称图形中最短路线问题,找出PC+PD值最小时点P的位置是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
6.$\frac{2}{3}$的倒数是( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
19.一个不透明的盒子中装有2个白球,3个红球和5个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出1个球,摸到红球的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
 图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
图是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )



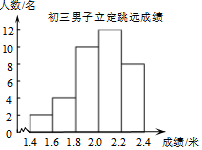 如图,为某校初三男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1:2:5:6:4,第四组的频数是12,对于下面的四种说法
如图,为某校初三男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1:2:5:6:4,第四组的频数是12,对于下面的四种说法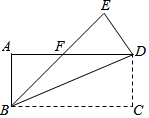 如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.
如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.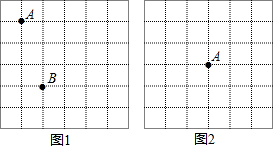
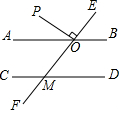 如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O,若∠AOP=30°,求∠EMD的度数.
如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O,若∠AOP=30°,求∠EMD的度数.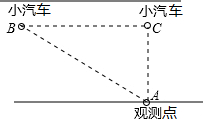 《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上的行驶速度不得超过70千米/时,如图,一辆小汽车在某城市街道直道上行驶,某一时刻刚好行驶到路对面车速检测仪A(观测点)正前方30米处的C处,过了2秒钟后,测得小汽车与车速检测仪间的距离为50米,问:这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上的行驶速度不得超过70千米/时,如图,一辆小汽车在某城市街道直道上行驶,某一时刻刚好行驶到路对面车速检测仪A(观测点)正前方30米处的C处,过了2秒钟后,测得小汽车与车速检测仪间的距离为50米,问:这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)