题目内容
1.已知点A(-1,-2)在反比例函数y=$\frac{k}{x}$ 的图象上,则当x>1时,y的取值范围是0<y<2.分析 先把A(-1,-2)代入反比例函数y=$\frac{k}{x}$,求出k的值,再由反比例函数的增减性即可得出结论.
解答 解:∵点A(-1,-2)在反比例函数y=$\frac{k}{x}$ 的图象上,
∴k=(-1)×(-2)=2>0,
∴函数图象的两个分支分别位于第一三象限,且在每一象限内y随x的增大而减小.
∵当x=1时,y=2,
∴当x>1时,0<y<2.
故答案为:0<y<2.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
11.下列各组长度的3条线段,不能构成三角形的是( )
| A. | 3cm,5cm,7cm | B. | 5cm,4cm,9cm | C. | 4cm,6cm,9cm | D. | 2cm,3cm,4cm |
12.如果x+y=4,那么代数式$\frac{2x}{{x}^{2}-{y}^{2}}$-$\frac{2y}{{x}^{2}-{y}^{2}}$的值是( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
16.若一组数据2,4,6,8,x的方差比另一组数据5,7,9,11,13的方差大,则 x 的值可以为( )
| A. | 12 | B. | 10 | C. | 2 | D. | 0 |
6.$\frac{2}{3}$的倒数是( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
19.一个不透明的盒子中装有2个白球,3个红球和5个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出1个球,摸到红球的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
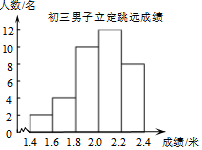 如图,为某校初三男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1:2:5:6:4,第四组的频数是12,对于下面的四种说法
如图,为某校初三男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1:2:5:6:4,第四组的频数是12,对于下面的四种说法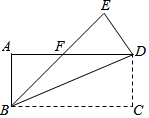 如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.
如图,把一张长方形纸片ABCD沿对角线BD折叠(长方形的对边平行且相等,每个角都相等),点C落在E处,BE交AD于F.判断三角形BDF的形状,并说明理由.