题目内容
1.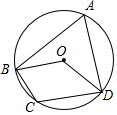 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )| A. | π | B. | $\frac{3}{2}π$ | C. | 2π | D. | 3π |
分析 由圆内接四边形的性质和圆周角定理求出∠A=60°,得出∠BOD=120°,再由弧长公式即可得出答案.
解答 解:∵四边形ABCD内接于⊙O,
∴∠BCD+∠A=180°,
∵∠BOD=2∠A,∠BOD=∠BCD,
∴2∠A+∠A=180°,
解得:∠A=60°,
∴∠BOD=120°,
∴$\widehat{BD}$的长=$\frac{120π×3}{180}$=2π;
故选:C.
点评 本题考查了弧长公式、圆内接四边形的性质、圆周角定理;熟练掌握圆内接四边形的性质和圆周角定理,求出∠BOD=120°是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
 某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 两点之间线段最短 | |
| B. | 两点确定一条直线 | |
| C. | 垂线段最短 | |
| D. | 经过直线外一点,有且只有一条直线与这条直线平行 |
12.下列说法正确的是( )
| A. | 调查孝感区居民对创建“全国卫生城市”的知晓度,宜采用抽样调查 | |
| B. | 一组数据85,95,90,95,95,90,90,80,95,90的众数为95 | |
| C. | “打开电视,正在播放乒乓球比赛”是必然事件 | |
| D. | 同时抛掷两枚质地均匀的硬币一次,出现两个正面朝上的概率为$\frac{1}{2}$ |
9. 如图的几何体,其左视图是( )
如图的几何体,其左视图是( )
 如图的几何体,其左视图是( )
如图的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
16.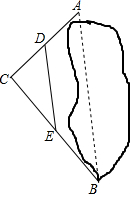 如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )
如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )
 如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )
如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )| A. | 50m | B. | 48m | C. | 45m | D. | 35m |
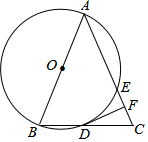 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F.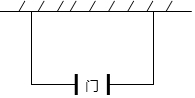 如图,某农场拟建一间饲养室,一面靠现有墙(墙足够长),且与现有墙相对的一侧墙体留有1m宽的门.已知计划中的材料可建墙体(不包括门)总长为11m,则能建成的饲养室总占地面积最大为( )m2.
如图,某农场拟建一间饲养室,一面靠现有墙(墙足够长),且与现有墙相对的一侧墙体留有1m宽的门.已知计划中的材料可建墙体(不包括门)总长为11m,则能建成的饲养室总占地面积最大为( )m2.