题目内容
18.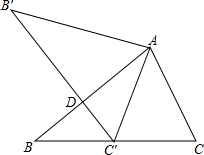 如图,将△ABC绕点A顺时针旋转60°后,得△AB′C,且C′为BC的中点,则$\frac{B′D}{AB′}$=$\frac{\sqrt{3}}{2}$.
如图,将△ABC绕点A顺时针旋转60°后,得△AB′C,且C′为BC的中点,则$\frac{B′D}{AB′}$=$\frac{\sqrt{3}}{2}$.
分析 先判断出△ABC是直角三角形,再判断出△ADB′也是直角三角形,在求出∠B′,最后用锐角三角函数求解即可.
解答 解:由性质的性质得,AC=AC′,∠CAC′=60°,∠B′=∠B
∴△ACC′是等边三角形,
∵点C′是BC中点,
∴BC′=CC′,
∴AC′=$\frac{1}{2}$BC,
∴△ABC是直角三角形,
∴∠BAC=∠B=30°
∴∠B′AD=60°,
∴∠ADB′=90°,
∴cos∠B′=$\frac{B′D}{AB′}$=cos30°=$\frac{\sqrt{3}}{2}$.
故答案为$\frac{\sqrt{3}}{2}$.
点评 此题是先行者性质的题,主要考查了直角三角形的判断和性质,等腰三角形的性质和判定和性质,解本题的关键是直角三角形的判断.

练习册系列答案
相关题目
20.某校举行“我爱我校”演讲比赛,由7名学生组成评委组.小明统计了每位评委对某参赛选手的评分并制成如下表格:
如果以去掉一个最高分和一个最低分后其他5名评委的平均分记为选手的最后得分,那么表中的数据一定不发生变化的是( )
| 众数 | 中位数 | 平均数 | 方差 |
| 7.9 | 8.3 | 8.2 | 0.3 |
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
6.若一个多边形的每个内角都为135°,则它的边数为( )
| A. | 6 | B. | 8 | C. | 5 | D. | 10 |
8.小明想做一个直角三角形的木架,以下四组木棒中,哪一组的三条能够刚好做成( )
| A. | 3cm,4cm,7cm | B. | 6cm,8cm,12cm | C. | 7cm,12cm,15cm | D. | 8cm,15cm,17cm |
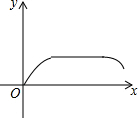
 如图,矩形MDBN从B点匀速向右运动,当B点与C点重合时停止,设移动的时间为x,两图形重合的面积为y,则y关于x的函数图象是( )
如图,矩形MDBN从B点匀速向右运动,当B点与C点重合时停止,设移动的时间为x,两图形重合的面积为y,则y关于x的函数图象是( )


 如图,三角形DEF平移得到三角形ABC,已知∠B=45°,∠C=65°,则∠FDE=70°.
如图,三角形DEF平移得到三角形ABC,已知∠B=45°,∠C=65°,则∠FDE=70°.