题目内容
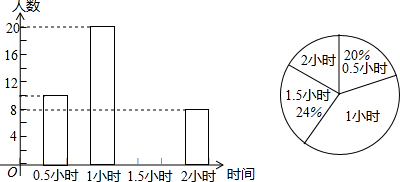
假期,学校组织部分学生分别到A、B、C、D四个地方夏令营,学校按定额购买了前往四地的车票,如图1,是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
(1)若去C地的车票占全部车票的30%,求去C地的车票数量是多少张?并补全统计图.
(2)若采取随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么小明抽到去B地的概率是多少?
(3)若有一张去A 地的车票,小亮和小红都想去,决定采取旋转转盘的方式来确定,其中甲转盘被分成四等分且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,如图2,具体规定是:同时转动两个转盘,当指向的两个数字之和是偶数时,票给小红,否则票给小亮(指针指在线上重转),试用“列表法”或“树状图”的方法分析这个规定对双方是否公平?

(1)若去C地的车票占全部车票的30%,求去C地的车票数量是多少张?并补全统计图.
(2)若采取随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么小明抽到去B地的概率是多少?
(3)若有一张去A 地的车票,小亮和小红都想去,决定采取旋转转盘的方式来确定,其中甲转盘被分成四等分且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,如图2,具体规定是:同时转动两个转盘,当指向的两个数字之和是偶数时,票给小红,否则票给小亮(指针指在线上重转),试用“列表法”或“树状图”的方法分析这个规定对双方是否公平?

考点:游戏公平性,条形统计图,列表法与树状图法
专题:计算题
分析:(1)根据去A、B、D的车票总数除以所占的百分比求出总数,再减去去A、B、D的车票总数即可;
(2)用去B地的车票数除以总的车票数即可;
(3)根据题意用列表法分别求出当指针指向的两个数字之和是偶数时的概率,即可求出这个规定对双方是否公平.
(2)用去B地的车票数除以总的车票数即可;
(3)根据题意用列表法分别求出当指针指向的两个数字之和是偶数时的概率,即可求出这个规定对双方是否公平.
解答: 解:(1)根据题意得:
解:(1)根据题意得:
总的车票数是:(20+40+10)÷(1-30%)=100,
则去C地的车票数量是100-70=30;
(2)小明抽到去B地的概率是:
=
;
(3)根据题意列表如下:
因为两个数字之和是偶数时的概率是
=
,
所以票给小红的概率是
,
所以这个规定对双方公平.
 解:(1)根据题意得:
解:(1)根据题意得:总的车票数是:(20+40+10)÷(1-30%)=100,
则去C地的车票数量是100-70=30;
(2)小明抽到去B地的概率是:
| 40 |
| 100 |
| 2 |
| 5 |
(3)根据题意列表如下:
| 1 | 2 | 3 | 4 | |
| 7 | 8 | 9 | 10 | 11 |
| 8 | 9 | 10 | 11 | 12 |
| 9 | 10 | 11 | 12 | 13 |
| 6 |
| 12 |
| 1 |
| 2 |
所以票给小红的概率是
| 1 |
| 2 |
所以这个规定对双方公平.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
相关题目
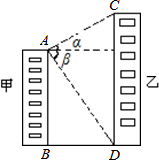 如图甲楼AB的高为40米,小华从甲楼顶A测乙楼顶C仰角为α=30°,观测乙楼的底部D俯角为β=45°;
如图甲楼AB的高为40米,小华从甲楼顶A测乙楼顶C仰角为α=30°,观测乙楼的底部D俯角为β=45°; 如图,AD∥BC,AB=AC,∠MAD=40°,则∠CAD=
如图,AD∥BC,AB=AC,∠MAD=40°,则∠CAD=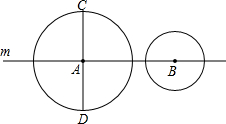 如图,⊙A的直径为8,⊙B的直径为6,A、B两点均在直线m上,且⊙A的直径CD与直线m垂直,当点B在直线m上移动时,设AB=d,若⊙B运动到和⊙A、CD都有交点时,d的取值范围是
如图,⊙A的直径为8,⊙B的直径为6,A、B两点均在直线m上,且⊙A的直径CD与直线m垂直,当点B在直线m上移动时,设AB=d,若⊙B运动到和⊙A、CD都有交点时,d的取值范围是