题目内容
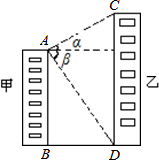 如图甲楼AB的高为40米,小华从甲楼顶A测乙楼顶C仰角为α=30°,观测乙楼的底部D俯角为β=45°;
如图甲楼AB的高为40米,小华从甲楼顶A测乙楼顶C仰角为α=30°,观测乙楼的底部D俯角为β=45°;(1)求甲、乙两楼之间的距离;
(2)求乙楼的高度(结果保留根号).
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:(1)过点A作AE⊥CD于E,可得四边形ABDE为矩形,根据β=45°,可得AE=DE=40米;
(2)在Rt△ACE中,根据α=30°,AE=40米,求出CE的长度,继而可求得乙楼的高度.
(2)在Rt△ACE中,根据α=30°,AE=40米,求出CE的长度,继而可求得乙楼的高度.
解答:解:(1)过点A作AE⊥CD于E,
则四边形ABDE为矩形,
∴DE=AB=40米,
∵β=45°,
∴AE=DE=40米
即两楼之间的距离为40米;
(2)在Rt△ACE中,
∵α=30°,AE=40米,
∴
=tan30°,
∴CE=40×
=
,
则楼高为:DE+CE=40+
(米).
答:乙楼的高度为(40+
)米.
则四边形ABDE为矩形,
∴DE=AB=40米,
∵β=45°,
∴AE=DE=40米
即两楼之间的距离为40米;
(2)在Rt△ACE中,
∵α=30°,AE=40米,
∴
| CE |
| AE |
∴CE=40×
| ||
| 3 |
40
| ||
| 3 |
则楼高为:DE+CE=40+
40
| ||
| 3 |
答:乙楼的高度为(40+
40
| ||
| 3 |
点评:本题考查了解直角三角形的应用,根据仰角和俯角构造直角三角形,利用三角函数求解是解答本题的关键.

练习册系列答案
相关题目
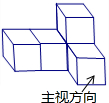 5个大小相同的正方体搭成的几何体如图,则下列说法中正确的是( )
5个大小相同的正方体搭成的几何体如图,则下列说法中正确的是( )| A、主视图的面积最小 |
| B、左视图的面积最小 |
| C、俯视图的面积最小 |
| D、三个视图面积一样大 |
 如图,已知AB是⊙O的直径,BC、EF是⊙O的弦,且EF垂直AB于点G,交BC于点H,CD与FE延长线交于D点,CD=DH.
如图,已知AB是⊙O的直径,BC、EF是⊙O的弦,且EF垂直AB于点G,交BC于点H,CD与FE延长线交于D点,CD=DH.
 小王和小明在课外活动中练习打羽毛球,球网(图中线段AB)在(6,0)处,高1.5米.
小王和小明在课外活动中练习打羽毛球,球网(图中线段AB)在(6,0)处,高1.5米. 如图,A、B是第二象限内双曲线y=
如图,A、B是第二象限内双曲线y=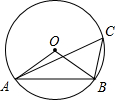 如图,OA,OB是⊙O的半径,点C在⊙O上,∠ACB=50°,则∠ABO的度数为
如图,OA,OB是⊙O的半径,点C在⊙O上,∠ACB=50°,则∠ABO的度数为 如图,在矩形ABCD中,AB=3,BC=4,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠BCD的平分线上时,则CA1的长为
如图,在矩形ABCD中,AB=3,BC=4,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠BCD的平分线上时,则CA1的长为