题目内容
 如图,AD∥BC,AB=AC,∠MAD=40°,则∠CAD=
如图,AD∥BC,AB=AC,∠MAD=40°,则∠CAD=考点:平行线的性质,等腰三角形的性质
专题:
分析:先根据平行线的性质求出∠ABC的度数,再由等腰三角形的性质求出∠C的度数,根据三角形内角和定理得出∠BAC的度数,进而得出结论.
解答:解:∵AD∥BC,∠MAD=40°,
∴∠ABC=∠MAD=40°,
∵AB=AC,
∴∠ABC=∠C=40°,
∴∠BAC=180°-40°-40°=100°,
∴∠CAD=180°-∠MAD-∠BAC=180°-40°-100°=40°.
故答案为:40°.
∴∠ABC=∠MAD=40°,
∵AB=AC,
∴∠ABC=∠C=40°,
∴∠BAC=180°-40°-40°=100°,
∴∠CAD=180°-∠MAD-∠BAC=180°-40°-100°=40°.
故答案为:40°.
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
现有点数为3,4,7,8的四张扑克牌,背面朝上洗匀,然后从中任意抽取两张,这两张牌上的数字之和为奇数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|

 小王和小明在课外活动中练习打羽毛球,球网(图中线段AB)在(6,0)处,高1.5米.
小王和小明在课外活动中练习打羽毛球,球网(图中线段AB)在(6,0)处,高1.5米. 如图,A、B是第二象限内双曲线y=
如图,A、B是第二象限内双曲线y=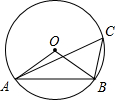 如图,OA,OB是⊙O的半径,点C在⊙O上,∠ACB=50°,则∠ABO的度数为
如图,OA,OB是⊙O的半径,点C在⊙O上,∠ACB=50°,则∠ABO的度数为