题目内容
9.把一次函数y=x-3的图象绕点(1,0)旋转180°,则所得直线的表达式为( )| A. | y=x+3 | B. | y=-x+3 | C. | y=x+1 | D. | y=x-1 |
分析 分别令x=0、y=0,可得出直线y=x-3与y轴、x轴的交点坐标,找出该两点绕点(1,0)旋转180°后的坐标,设旋转后所得直线的表达式为y=kx+b,结合点的坐标利用待定系数法即可得出结论.
解答 解:令x=0,则y=-3,
即直线y=x-3与y轴交点为(0,-3);
令y=0,则有x-3=0,解得:x=3,
即直线y=x-3与x轴交点为(3,0).
点(0,-3)绕点(1,0)旋转180°变为(2,3),点(3,0)绕点(1,0)旋转180°变为(-1,0).
令旋转后所得直线的表达式为y=kx+b,
则有$\left\{\begin{array}{l}{2k+b=3}\\{-k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$.
故旋转后所得直线的表达式为y=x+1.
故选C.
点评 本题考查了一次函数图象与几何变换,解题的关键是找出直线y=x-3与y轴、x轴的交点坐标绕点(1,0)旋转180°后的新坐标.本题属于基础题,难度不大,解决该题型题目时,先求出直线与坐标轴的交点,找出交点旋转后的新坐标再利用待定系数法即可得出旋转后的函数解析式.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
17.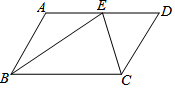 如图,在平行四边形ABCD中,AD=10 cm,CD=6 cm,E为AD上任意的一点,且BE=BC,CE=CD,则DE的长度是( )
如图,在平行四边形ABCD中,AD=10 cm,CD=6 cm,E为AD上任意的一点,且BE=BC,CE=CD,则DE的长度是( )
 如图,在平行四边形ABCD中,AD=10 cm,CD=6 cm,E为AD上任意的一点,且BE=BC,CE=CD,则DE的长度是( )
如图,在平行四边形ABCD中,AD=10 cm,CD=6 cm,E为AD上任意的一点,且BE=BC,CE=CD,则DE的长度是( )| A. | 3 cm | B. | 3.5 cm | C. | 3.6 cm | D. | 4 cm |
4.10名学生的身高如下(单位:cm)159、169、163、170、166、165、156、172、165、162,从中任选一名学生,其身高超过165cm的概率是( )
| A. | 0.5 | B. | 0.4 | C. | 0.2 | D. | 0.1 |
14.下列命题是真命题的是( )
| A. | 菱形的对角线互相平分 | |
| B. | 一组对边平行,一组对边相等的四边形是平行四边形 | |
| C. | 对角线互相垂直且相等的四边形是正方形 | |
| D. | 对角线相等的四边形是矩形 |
1.在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:
(1)请估计:当次数s很大时,摸到白球的频率将会接近0.3;假如你去摸一次,你摸到白球的概率是0.7(精确到0.1).
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
| 摸球的次数s | 150 | 200 | 500 | 900 | 1000 | 1200 |
| 摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
| 摸到白球的频率$\frac{n}{s}$ | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
18.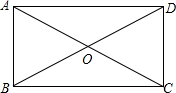 如图,下列条件中,能使?ABCD成为矩形是( )
如图,下列条件中,能使?ABCD成为矩形是( )
 如图,下列条件中,能使?ABCD成为矩形是( )
如图,下列条件中,能使?ABCD成为矩形是( )| A. | AB=AD | B. | ∠ABO=60° | C. | AO=BO | D. | AC⊥BD |
19.要使式子$\frac{{\sqrt{x+2}}}{x-1}$有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x≤-2 | C. | x≥1 | D. | x≥-2 且x≠1 |