题目内容
1.在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:| 摸球的次数s | 150 | 200 | 500 | 900 | 1000 | 1200 |
| 摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
| 摸到白球的频率$\frac{n}{s}$ | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
分析 (1)从表中的统计数据可知,摸到白球的频率稳定在0.3左右,而摸到红球的概率为1-0.3=0.7;
(2)根据红球的概率公式得到相应方程求解即可;
(3)言之有理即可.
解答 解:(1)0.3,1-0.3=0.7;
故答案是:0.3;0.7.
(2)估算口袋中红球有x只,
由题意得0.7=$\frac{x}{x+30}$,
解之得x=70,
∴估计口袋中红球有70只;
(3)用概率可以估计未知物体的数目.(或者试验次数很大时事件发生的频率作为概率的近似值)(只要能从概率方面说的合理即可).
点评 考查利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:概率=所求情况数与总情况数之比.组成整体的几部分的概率之和为1.

练习册系列答案
相关题目
5.计算:|-$\frac{1}{3}}$|=( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
12.使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点.已知函数y=x2-2mx-2(m+3)(m为常数),则该函数的零点的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 不能确定 |
9.把一次函数y=x-3的图象绕点(1,0)旋转180°,则所得直线的表达式为( )
| A. | y=x+3 | B. | y=-x+3 | C. | y=x+1 | D. | y=x-1 |
16. 如图是某几何体的三视图,则与该三视图相对应的几何体是( )
如图是某几何体的三视图,则与该三视图相对应的几何体是( )
 如图是某几何体的三视图,则与该三视图相对应的几何体是( )
如图是某几何体的三视图,则与该三视图相对应的几何体是( )| A. |  | B. |  | C. |  | D. |  |
13.已知实数a,b满足|2017-a|+$\sqrt{a-2018}$=a,则代数式a-20172=( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
10.为了了解某班学生每周使用零花钱的情况,小红随机调查了15名同学,结果如下表:
则这15名同学每周使用零花钱的众数和中位数分别是( )
| 每周使用零花钱(单位:元) | 10 | 20 | 30 | 50 | 60 |
| 人 数 | 2 | 5 | 4 | 3 | 1 |
| A. | 5,4 | B. | 20,30 | C. | 5,5 | D. | 20,20 |
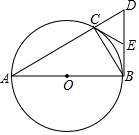 如图,已知△ABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
如图,已知△ABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.