题目内容
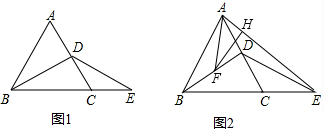
1. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC面积是27cm2,AB=10cm,AC=8cm.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC面积是27cm2,AB=10cm,AC=8cm.(1)求证:DE=DF;
(2)求DE的长.
分析 (1)根据全等三角形的判定和性质即可得到结论;
(2)根据角平分线上的点到角的两边距离相等可得DE=DF,然后利用△ABC的面积列方程求解即可.
解答 解:(1)∵AD为∠BAC的平分线,
∴∠BAD=∠CAD,
在 △ADE与△AFD中,$\left\{\begin{array}{l}{∠EAD=∩FAD}\\{∠AED=∠AFD=90°}\\{AD=AD}\end{array}\right.$,
△ADE与△AFD中,$\left\{\begin{array}{l}{∠EAD=∩FAD}\\{∠AED=∠AFD=90°}\\{AD=AD}\end{array}\right.$,
∴△AED≌△AFD,
∴DE=DF;
(2)∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵△ABC的面积是27cm2,AB=10cm,AC=8cm,
∴$\frac{1}{2}$×10•DE+$\frac{1}{2}$×8•DF=27,
解得DE=3cm.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并根据三角形的面积列出方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目