题目内容
1.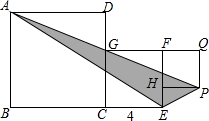 已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是16.
已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是16.
分析 连接AC、GE、PF.由AC∥GE∥PF,得S△EGA=S△EGC,S△EGP=S△EGF,由此即可解决问题.
解答 解:如图连接 AC、GE、PF.
AC、GE、PF.
∵四边形ABCD、四边形EFGC、四边形PQFH是正方形,
∴∠ACD=∠CGE=45°,∠GEF=∠EFP=45°,
∴AC∥GE∥PF,
∴S△EGA=S△EGC,S△EGP=S△EGF,
∴S△AEP=S△EGA+S△EGP=S△EGC+S△EGF=S正方形EFGC=16.
故答案为16.
点评 本题考查正方形的性质、平行线的性质等知识,解题的关键是利用等底同高的两个三角形面积相等解决问题,属于中考常考题型.

练习册系列答案
相关题目
12.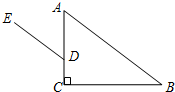 如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )
如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )
 如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )
如图,在△ABC中,∠C=90°,点D在AC边上,DE∥AB,如果∠ADE=46°,那么∠B等于( )| A. | 34° | B. | 54° | C. | 46° | D. | 44° |
10.下列运算中,正确的是( )
| A. | a2•a3=a5 | B. | a8÷a4=a2 | C. | (a5)2=a7 | D. | 2a+3b=5ab |

 如图,将正偶数按照图中所示的规律排列下去,若用有序实数对(a,b)表示第a行的第b个数.如(3,2)表示偶数10.
如图,将正偶数按照图中所示的规律排列下去,若用有序实数对(a,b)表示第a行的第b个数.如(3,2)表示偶数10. 已知实数a、b、c在数轴上的位置如图所示,a、b到原点的距离相等,化简:$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|
已知实数a、b、c在数轴上的位置如图所示,a、b到原点的距离相等,化简:$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{(c-a)^{2}}$+|b-c|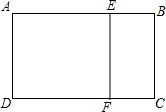 如图,矩形ABCD中,AB=6,BC=4,点E在AB上,EF⊥DC于点F,在边AD,DF,EF,AE上分别存在点M,N,P,Q,这四点构成的四边形与矩形BCFE全等,则DM的长度为$\sqrt{7}$.
如图,矩形ABCD中,AB=6,BC=4,点E在AB上,EF⊥DC于点F,在边AD,DF,EF,AE上分别存在点M,N,P,Q,这四点构成的四边形与矩形BCFE全等,则DM的长度为$\sqrt{7}$.