题目内容
13.(1)计算:(-1)3+($\frac{1}{2}$)-2-$\sqrt{12}$×$\sqrt{3}$;(2)化简:($\frac{1}{{x}^{2}-1}$+1)•$\frac{{x}^{2}+2x+1}{{x}^{2}}$.
分析 (1)原式利用乘方的意义,负整数指数幂法则,以及二次根式乘法法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,约分即可得到结果.
解答 解:(1)原式=-1+4-6=-7+4=-3;
(2)原式=$\frac{{x}^{2}}{{x}^{2}-1}$•$\frac{(x+1)^{2}}{{x}^{2}}$=$\frac{{x}^{2}}{(x+1)(x-1)}$•$\frac{(x+1)^{2}}{{x}^{2}}$=$\frac{x+1}{x-1}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列运算结果为负数的是( )
| A. | -(-2) | B. | (-2)2 | C. | |-2| | D. | (-2)3 |
4.下列计算正确的是( )
| A. | a4÷a3=1 | B. | a4+a3=a7 | C. | (2a3)4=8a12 | D. | a4•a3=a7 |
18.下列运算中,结果是a6的式子是( )
| A. | (a3)3 | B. | a12-a6 | C. | a2•a3 | D. | (-a)6 |
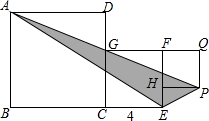 已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是16.
已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是16.
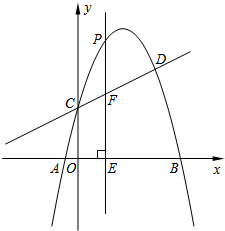 如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+2交于C,D两点,其中点C在y轴上,点D的横坐标为3,点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+2交于C,D两点,其中点C在y轴上,点D的横坐标为3,点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.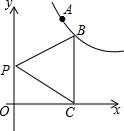 已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点
已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点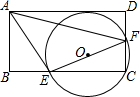 如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.
如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.