题目内容
11.抛物线y=8(x-k)2的顶点P在x轴上,与y轴交于点Q,且PQ=$\frac{\sqrt{17}}{2}$,求此抛物线的函数解析式及△PQ0的面积.分析 由y=8(x-k)2知点P(k,0)、Q(0,8k2),根据OP2+OQ2=PQ2得关于k的方程,解方程可得k的值,即可得抛物线解析式,进而知OP、OQ,列式即可计算S△PQO.
解答 解:根据题意知点P坐标为(k,0),
当x=0时,y=8k2,
∴点Q坐标为(0,8k2),
∵OP2+OQ2=PQ2,PQ=$\frac{\sqrt{17}}{2}$,
∴k2+64k4=$\frac{17}{4}$,即256k4+4k2-17=0,
解得:k2=$\frac{1}{4}$或k2=-$\frac{17}{64}$(舍),
∴k=$\frac{1}{2}$或k=-$\frac{1}{2}$,
故抛物线解析式为:y=8(x-$\frac{1}{2}$)2或y=8(x+$\frac{1}{2}$)2;
当k=$\frac{1}{2}$或k=-$\frac{1}{2}$时,OP=$\frac{1}{2}$,OQ=2,
∴S△PQO=$\frac{1}{2}$×OP×OQ=$\frac{1}{2}$×$\frac{1}{2}$×2=$\frac{1}{2}$.
点评 本题主要考查待定系数法求二次函数解析式及勾股定理的运用,根据解析式表示点P、Q的坐标是根本,由勾股定理得出关于k的方程是关键.

练习册系列答案
相关题目
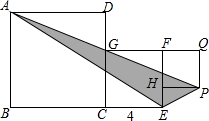 已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是16.
已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是16.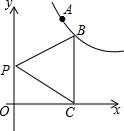 已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点
已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点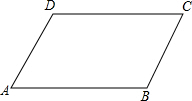 如图,已知平行四边形ABCD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示下列向量:
如图,已知平行四边形ABCD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示下列向量: 一个由若干个相同的正方体组成的几何体,其主视图和左视图如图所示,这个几何体最少可以由10个这样的正方体组成.
一个由若干个相同的正方体组成的几何体,其主视图和左视图如图所示,这个几何体最少可以由10个这样的正方体组成.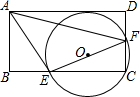 如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.
如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.