题目内容
11. 如图,AB=AC,点D,E分别在AB,AC上,请添加一个条件BD=EC或∠B=∠C,即可推出OD=OE.
如图,AB=AC,点D,E分别在AB,AC上,请添加一个条件BD=EC或∠B=∠C,即可推出OD=OE.
分析 结论:BD=EC或∠B=∠C,关键是证明△BOD≌△COE.
解答 解:当BD=DE时,∵AB=AC,
∴AE=AD,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AE=AD}\\{∠A=∠A}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD,
∴∠B=∠C,
在△BOC和△COE中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠DOB=∠EOC}\\{BD=EC}\end{array}\right.$,
∴△BOD≌△COE,
∴DO=OE,
当∠B=∠C时,先证明△ABE≌△ACD,再证明△BOD≌△COE,即可推出DO=OE.
点评 本题考查全等三角形的判定和性质,解题的关键是灵活运用全等三角形的判定和性质,属于基础题,中考常考题型.

练习册系列答案
相关题目
15.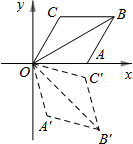 如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )
如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )
 如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )
如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )| A. | (3,$\sqrt{3}$) | B. | (3,-$\sqrt{3}$) | C. | ($\sqrt{6}$,$\sqrt{6}$) | D. | ($\sqrt{6}$,-$\sqrt{6}$) |
16.在比例尺为1:80000的江阴市地图上,长山大道的长度约为25cm,它的实际长度约为( )
| A. | 200m | B. | 20m | C. | 20km | D. | 200km |
20.一辆列车通过隧道,从车头进车尾出隧道共用1分30秒,已知列车的速度为100千米/时,列车长100米.则隧道长为( )
| A. | 2.5千米 | B. | 1.5千米 | C. | 2.4千米 | D. | 14.9千米 |
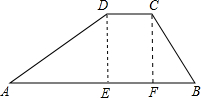 如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.
如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.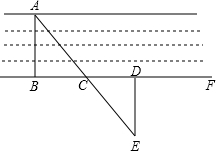 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线,并在这条垂线上取一点E,使A、C、E在一条直线上(如图所示),测得ED的长就是A、B之间的距离,请你说明理由.
如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线,并在这条垂线上取一点E,使A、C、E在一条直线上(如图所示),测得ED的长就是A、B之间的距离,请你说明理由.