题目内容
5.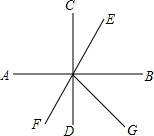 如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )
如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )| A. | 90° | B. | 60° | C. | 30° | D. | 无法确定 |
分析 利用垂线的性质结合对顶角的性质得出∠GOE=∠DOG=∠FOD进而得出答案.
解答  解:∵AB⊥CD,OB平分∠EOG,
解:∵AB⊥CD,OB平分∠EOG,
∴∠COB=∠BOD=90°,∠EOB=∠GOB,
∴∠COE=∠GOD,
∵∠FOD=60°,
∴∠GOE=∠DOG=∠FOD=60°,
∴∠BOG=30°.
故选:C.
点评 此题主要考查了垂线的定义以及对顶角,正确把握相关定义是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.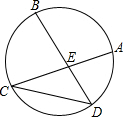 如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )
如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )
 如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )
如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 15° |
10.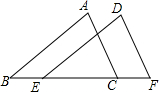 如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )
如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )
 如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )
如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )| A. | AB=DE | B. | ∠A=∠D | C. | AC∥DF | D. | AC=DF |
17.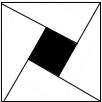 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的之边长为1,则图中阴影部分的面积为( )
由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的之边长为1,则图中阴影部分的面积为( )
 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的之边长为1,则图中阴影部分的面积为( )
由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的之边长为1,则图中阴影部分的面积为( )| A. | 1 | B. | 3 | C. | 4-2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
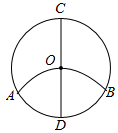 如图,CD为⊙O的直径,以D为圆心,DO长为半径作弧,交⊙O于两点A、B,证明:$\widehat{AC}$=$\widehat{CB}$=$\widehat{BDA}$.
如图,CD为⊙O的直径,以D为圆心,DO长为半径作弧,交⊙O于两点A、B,证明:$\widehat{AC}$=$\widehat{CB}$=$\widehat{BDA}$. 有理数a,b在数轴上如图,用“<”把b+a,b-a,a-b,-a-b按从小到大的顺序连接起来.
有理数a,b在数轴上如图,用“<”把b+a,b-a,a-b,-a-b按从小到大的顺序连接起来. 如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2).以点A为圆心,AB长为半径画弧,交AC于点D,则点D的坐标为(3-$\sqrt{13}$,2).
如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2).以点A为圆心,AB长为半径画弧,交AC于点D,则点D的坐标为(3-$\sqrt{13}$,2).
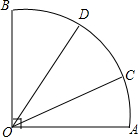 如图,∠AOB=90°,OA=OB,C、D是$\widehat{AB}$上的两点,∠AOD>∠AOC.
如图,∠AOB=90°,OA=OB,C、D是$\widehat{AB}$上的两点,∠AOD>∠AOC.