题目内容
3.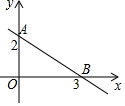 如图,直线AB对应的函数表达式是( )
如图,直线AB对应的函数表达式是( )| A. | y=-$\frac{3}{2}$x+2 | B. | y=$\frac{3}{2}$x+3 | C. | y=-$\frac{2}{3}$x+2 | D. | y=$\frac{2}{3}$x+2 |
分析 根据点A、B的坐标,利用待定系数法求出直线AB对应的函数表达式,此题得解.
解答 解:设直线AB对应的函数表达式为y=kx+b(k≠0),
将A(0,2)、B(3,0)代入y=kx+b中,
$\left\{\begin{array}{l}{b=2}\\{3k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=2}\end{array}\right.$,
∴直线AB对应的函数表达式为y=-$\frac{2}{3}$x+2.
故选C.
点评 本题考查了待定系数法求一次函数解析式,熟练掌握利用待定系数法求函数解析式的步骤及方法是解题的关键.

练习册系列答案
相关题目
13. 如图,∠CAB=∠DBA,再添加一个条件不一定能判定△ABC≌△BAD的是( )
如图,∠CAB=∠DBA,再添加一个条件不一定能判定△ABC≌△BAD的是( )
 如图,∠CAB=∠DBA,再添加一个条件不一定能判定△ABC≌△BAD的是( )
如图,∠CAB=∠DBA,再添加一个条件不一定能判定△ABC≌△BAD的是( )| A. | ∠DAB=∠CBA | B. | AD=BC | C. | AC=BD | D. | ∠C=∠D |

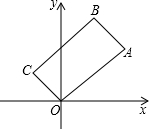 在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离. 如图,DE,BC被那条直线所截,得到哪些同位角,内错角或同旁内角?请一一指出.
如图,DE,BC被那条直线所截,得到哪些同位角,内错角或同旁内角?请一一指出.