题目内容
化简求值;
(1)x2-
-[x-
(x2+x)],其中x=2.
(2)
a2b-5ac-(3a2c-a2b)+(3ac-4a2c),其中a=1,b=2,c=2.
(1)x2-
| 1 |
| 2 |
| 1 |
| 2 |
(2)
| 1 |
| 2 |
考点:整式的加减—化简求值
专题:
分析:(1)根据去括号的法则,可去掉括号,根据合并同类项的法则,可化简整式,根据代数式求值,可得答案;
(2)根据去括号的法则,可去掉括号,根据合并同类项的法则,可化简整式,根据代数式求值,可得答案.
(2)根据去括号的法则,可去掉括号,根据合并同类项的法则,可化简整式,根据代数式求值,可得答案.
解答:解:(1)原式=x2-
-[x-
x2-
x]
=x2-
-x+
x2+
=
x2-
x+
,
当=2时,原式=
×22-
×2+
=6-1+
=
;
(2)原式=
a2b-5ac-3a2c+a2b+3ac-4a2c
=(
a2b+a2b)+(-5ac+3ac)+(-3a2c-4a2c)
=
a2b-2ac-7a2c,
当a=1,b=2,c=2时,原式=
×1×2-2×1×2-7×1×2=3-4-14=-15.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=x2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当=2时,原式=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 2 |
(2)原式=
| 1 |
| 2 |
=(
| 1 |
| 2 |
=
| 3 |
| 2 |
当a=1,b=2,c=2时,原式=
| 3 |
| 2 |
点评:本题考查了整式的化简求值,去括号:括号前是正数去括号不变号,括号前是负数去括号全变号.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知OC是∠AOB的平分线,则下列结论不正确的是( )
| A、∠AOC=∠BOC | ||
B、∠AOC=
| ||
| C、∠AOB=2∠BOC | ||
| D、∠AOB=∠BOC |
已知α为锐角,且cosα≤sin30°,则( )
| A、0°≤α≤60° |
| B、60°≤α<90° |
| C、0°<α≤30° |
| D、30°≤α<90° |
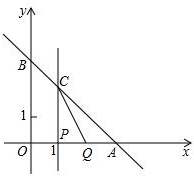 已知直线y=-x+3分别交x轴,y轴于A,B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,线段OA上另有一动点Q由点A向点O运动,它与点P以同样速度同时出发,当点P到达点A时两点同时停止运动(如图),设运动时间为t秒.
已知直线y=-x+3分别交x轴,y轴于A,B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,线段OA上另有一动点Q由点A向点O运动,它与点P以同样速度同时出发,当点P到达点A时两点同时停止运动(如图),设运动时间为t秒. 如图:
如图: