题目内容
12.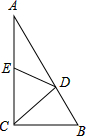 如图,在△ABC中,∠ACB=90°,点D在AB边上,连接CD,将△BCD沿CD翻折得到△ECD,点B的对称点E恰好落在AC边上,若∠B=55°,则∠ADE的度数是20°.
如图,在△ABC中,∠ACB=90°,点D在AB边上,连接CD,将△BCD沿CD翻折得到△ECD,点B的对称点E恰好落在AC边上,若∠B=55°,则∠ADE的度数是20°.
分析 先根据三角形内角和定理计算出∠A的度数,再根据折叠的性质得∠DEC=∠B=55°,然后根据三角形外角性质求∠ADE的度数.
解答 解:∵∠ACB=90°,∠B=55°,
∴∠A=90°-55°=35°,
∵沿CD折叠△CBD,使点B恰好落在AC边上的点E处,
∴∠DEC=∠B=55°,
∵∠DEC=∠A+∠ADE,
∴∠ADE=55°-35°=20°.
故答案为:20°.
点评 本题考查的是翻折变换和三角形内角和定理,三角形外角性质;理解翻折变换的性质、熟记三角形外角性质是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
2.y=kx+b中,当x=1时y=2;当x=2时y=4,则k,b的值是( )
| A. | $\left\{\begin{array}{l}k=0\\ b=0\end{array}\right.$ | B. | $\left\{\begin{array}{l}k=2\\ b=0\end{array}\right.$ | C. | $\left\{\begin{array}{l}k=3\\ b=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=0\\ b=2\end{array}\right.$ |
17.对抛物线y=-x2+2x-3,下列结论正确的是( )
| A. | 有最低点 | B. | 开口向上 | ||
| C. | 与y轴交点坐标是(0,3) | D. | 顶点坐标是(1,-2) |
1.使分式$\frac{3}{x-3}$=$\frac{3(x+3)}{{x}^{2}-9}$自左向右变形成立的条件( )
| A. | x>-3 | B. | x<-3 | C. | x≠-3 | D. | x≠3 |

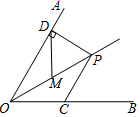 如图,点P在∠AOB的角平分线上,∠AOB=60°,PD⊥OA于D,M在OP上,且DM=MP=4,若C是OB上的动点,则PC的最小值是( )
如图,点P在∠AOB的角平分线上,∠AOB=60°,PD⊥OA于D,M在OP上,且DM=MP=4,若C是OB上的动点,则PC的最小值是( )