题目内容
2.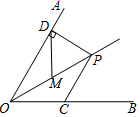 如图,点P在∠AOB的角平分线上,∠AOB=60°,PD⊥OA于D,M在OP上,且DM=MP=4,若C是OB上的动点,则PC的最小值是( )
如图,点P在∠AOB的角平分线上,∠AOB=60°,PD⊥OA于D,M在OP上,且DM=MP=4,若C是OB上的动点,则PC的最小值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 根据角平分线的定义可得∠AOP=$\frac{1}{2}$AOB=30°,求出DM=OM=4,再根据直角三角形的性质求得PD=$\frac{1}{2}$OP=4,然后根据角平分线的性质和垂线段最短得到结果.
解答 解:∵P是∠AOB角平分线上的一点,∠AOB=60°,
∴∠AOP=$\frac{1}{2}$∠AOB=30°,
∴∠DPO=60°,
∵PM=DM=4cm,
∴∠MDP=∠DPM=60°,
∵∠PDO=90°,
∴∠ODM=30°=∠AOP,
∴OM=DM=4,
∴OP=8,
∴PD=$\frac{1}{2}$OP=4,
∵点C是OB上一个动点,
∴PC的最小值为P到OB距离,
∴PC的最小值=PD=4,
故选C.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形的性质,熟记性质并作出辅助线构造成直角三角形是解题的关键.

练习册系列答案
相关题目
13.对下列问题进行调查时采用的方式适合普查的是( )
| A. | 工厂对准备出厂的一批轿车的刹车系统进行测试 | |
| B. | 对某市九年级学生的视力调查 | |
| C. | 某质检部门调查某罐头厂生产的一批罐头的质量 | |
| D. | 对某厂生产的摩托车头盔进行防撞击性能测试 |
7.小李打羽毛球时,若羽毛球飞行的高度h(m)与发球的时间t(s)满足关系式h=-2t2+2t+2,则小李发球后0.5s时,羽毛球飞行的高度为( )
| A. | 1.5m | B. | 2m | C. | 2.5m | D. | 3m |
14.若三角形的两条边的长度是4cm和9cm,则第三条边的长度可能是( )
| A. | 4 cm | B. | 5 cm | C. | 9 cm | D. | 13 cm |
11.若关于x的方程ax-b=0(a≠0)的解为x=3,则一次函数y=ax-b(a≠0)的图象与x轴的交点坐标为( )
| A. | (-3,0) | B. | (3,0) | C. | (a,0) | D. | (-b,0) |
12.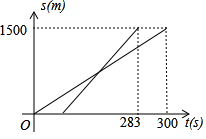 甲、乙两名同学在一次晨跑练习中都以各自的速度匀速跑,路程s(m)和时间t(s)之间的函数图象如图所示(粗线为甲的路程与时间的函数图象,细线为乙的路程与时间的函数图象),小张根据图象得到了如下四个信息,期中错误的是( )
甲、乙两名同学在一次晨跑练习中都以各自的速度匀速跑,路程s(m)和时间t(s)之间的函数图象如图所示(粗线为甲的路程与时间的函数图象,细线为乙的路程与时间的函数图象),小张根据图象得到了如下四个信息,期中错误的是( )
 甲、乙两名同学在一次晨跑练习中都以各自的速度匀速跑,路程s(m)和时间t(s)之间的函数图象如图所示(粗线为甲的路程与时间的函数图象,细线为乙的路程与时间的函数图象),小张根据图象得到了如下四个信息,期中错误的是( )
甲、乙两名同学在一次晨跑练习中都以各自的速度匀速跑,路程s(m)和时间t(s)之间的函数图象如图所示(粗线为甲的路程与时间的函数图象,细线为乙的路程与时间的函数图象),小张根据图象得到了如下四个信息,期中错误的是( )| A. | 这是一次1500m的赛跑 | B. | 甲、乙两人中先到达终点的是乙 | ||
| C. | 甲、乙同时起跑 | D. | 甲在这次赛跑中的速度为5m/s |
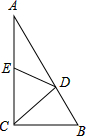 如图,在△ABC中,∠ACB=90°,点D在AB边上,连接CD,将△BCD沿CD翻折得到△ECD,点B的对称点E恰好落在AC边上,若∠B=55°,则∠ADE的度数是20°.
如图,在△ABC中,∠ACB=90°,点D在AB边上,连接CD,将△BCD沿CD翻折得到△ECD,点B的对称点E恰好落在AC边上,若∠B=55°,则∠ADE的度数是20°.
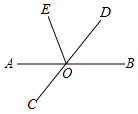 如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠BOE=110°.
如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠BOE=110°.