题目内容
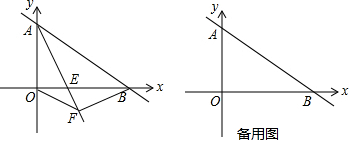
4.如图,是五角星和它的变形,(1)图①中是一个五角星,求∠A+∠B+∠C+∠D+∠E.
(2)图①中的点A向下移到BE上时,如图②,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?说明你结论的正确性.
(3)把图②中的点C向上移到BD上时,如图③,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化?说明你结论的正确性.

分析 (1)如图,连接CD,把五个角和转化为同一个三角形内角和.根据三角形中一个外角等于与它不相邻的两个内角和,再根据三角形内角和定理可得.
(2)、(3)五个角转化为一个平角.
解答  解:(1)如图,连接CD.
解:(1)如图,连接CD.
在△ACD中,根据三角形内角和定理,得出∠A+∠2+∠3+∠ACE+∠ADB=180°.
∵∠1=∠B+∠E=∠2+∠3,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°;
(2)无变化.
根据平角的定义,得出∠BAC+∠CAD+∠DAE=180°.
∵∠BAC=∠C+∠E,∠EAD=∠B+∠D,
∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°;
(3)无变化.
∵∠ACB=∠CAD+∠D,∠ECD=∠B+∠E,
∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°.
点评 本题考查的是三角形外角的性质及三角形内角和定理,利用了转化思想求解,(1)是把五个角转化在一个三角形中求解,(2)(3)是把五个角转化为一个平角求解.

练习册系列答案
相关题目
19.下列方程中,是一元二次方程的是( )
| A. | x2=0 | B. | ax2+bx+c=0(a,b,c均为常数) | ||
| C. | x2+y=5 | D. | x3+$\frac{2}{x}$+1=0 |
9.邻补角是( )
| A. | 和为180°的两个角 | |
| B. | 有公共顶点且有一条公共边,另一边互为反向延长线的两个角 | |
| C. | 有一条公共边且相等的两个角 | |
| D. | 有公共顶点且互补的两个角 |
16.已知$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$≠0,则$\frac{c-a}{b}$的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
13.对下列问题进行调查时采用的方式适合普查的是( )
| A. | 工厂对准备出厂的一批轿车的刹车系统进行测试 | |
| B. | 对某市九年级学生的视力调查 | |
| C. | 某质检部门调查某罐头厂生产的一批罐头的质量 | |
| D. | 对某厂生产的摩托车头盔进行防撞击性能测试 |
14.若三角形的两条边的长度是4cm和9cm,则第三条边的长度可能是( )
| A. | 4 cm | B. | 5 cm | C. | 9 cm | D. | 13 cm |
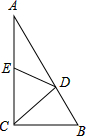 如图,在△ABC中,∠ACB=90°,点D在AB边上,连接CD,将△BCD沿CD翻折得到△ECD,点B的对称点E恰好落在AC边上,若∠B=55°,则∠ADE的度数是20°.
如图,在△ABC中,∠ACB=90°,点D在AB边上,连接CD,将△BCD沿CD翻折得到△ECD,点B的对称点E恰好落在AC边上,若∠B=55°,则∠ADE的度数是20°.