题目内容
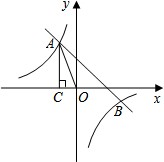 如图,直线y=ax+b与双曲线y=
如图,直线y=ax+b与双曲线y=| k |
| x |
| 3 |
| 2 |
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请利用函数图象直接写出y1,y2,y3之间满足的大小关系式.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)先根据反比例函数k的几何意义得到
|k|=
,易得k=-3,所以反比例函数解析式为y=-
,再利用反比例函数解析式确定A点和B点坐标,然后利用待定系数法求直线解析式;
(2)根据反比例函数的性质求解.
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| x |
(2)根据反比例函数的性质求解.
解答:解:(1)∵S△AOC=
,
∴
|k|=
,
而k<0,
∴k=-3,
∴反比例函数解析式为y=-
,
把A(m,3),B(3,n)代入y=-
得3m=3,3n=3,解得m=1,n=1,
∴A点坐标为(1,3),B点坐标为(3,1),
把A(1,3)、B(3,1)代入y=ax+b得
,解得
,
∴直线解析式为y=-x+4;
(2)当x1<x2<0<x3,y3<y1<y2.
| 3 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
| 2 |
而k<0,
∴k=-3,
∴反比例函数解析式为y=-
| 3 |
| x |
把A(m,3),B(3,n)代入y=-
| 3 |
| x |
∴A点坐标为(1,3),B点坐标为(3,1),
把A(1,3)、B(3,1)代入y=ax+b得
|
|
∴直线解析式为y=-x+4;
(2)当x1<x2<0<x3,y3<y1<y2.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及反比例函数的性质.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,二次函数y=ax2-
如图,二次函数y=ax2-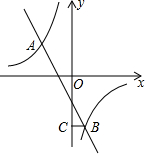 如图,在平面直角坐标系中,双曲线y=
如图,在平面直角坐标系中,双曲线y=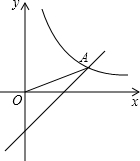 已知:在平面直角坐标系xOy中,直线y=x-4k与双曲线y=
已知:在平面直角坐标系xOy中,直线y=x-4k与双曲线y=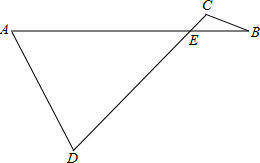 已知:AB、CD交于E点,连接AD、BC,
已知:AB、CD交于E点,连接AD、BC,