题目内容
 如图,二次函数y=ax2-
如图,二次函数y=ax2-| 3 |
| 2 |
(1)求抛物线的函数解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)此抛物线上是否存在点P,使得以P、A、C、B为顶点的四边形为梯形?若存在,请写出所有符合条件的P点坐标;若不存在,请说明理由;
(4)若点M是线段BC下方的抛物线上的一个动点,求△MBC面积的最大值以及此时点M的坐标.
考点:二次函数综合题
专题:
分析:(1)点A、C的坐标代入解析式中即可;
(2)利用△OAC∽△OCB或勾股定理逆定理,判断出△ABC为直角三角形;外接圆的圆心为AB的中点,且坐标为(
,0);
(3)根据梯形的定义,分①AB是底边时,PC∥AB,利用点P的纵坐标与点C的纵坐标相等,代入抛物线解析式计算求出点P的横坐标,即可得解;②AC是底边时,PB∥AC,先根据点A、C的坐标得到直线AC的解析式,再根据平行直线的解析式的k值相等求出过点B与AC平行的直线的解析式,然后与抛物线解析式联立求解即可得到点P的坐标;③BC是底边时,AP∥BC,根据点B、C的坐标求出直线BC的解析式,再根据平行直线的解析式的k值相等求出过点A与BC平行的直线的解析式,然后与抛物线解析式联立求解即可得到点P的坐标;
(4)△MBC的面积可由S△MBC=
BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
(2)利用△OAC∽△OCB或勾股定理逆定理,判断出△ABC为直角三角形;外接圆的圆心为AB的中点,且坐标为(
| 3 |
| 2 |
(3)根据梯形的定义,分①AB是底边时,PC∥AB,利用点P的纵坐标与点C的纵坐标相等,代入抛物线解析式计算求出点P的横坐标,即可得解;②AC是底边时,PB∥AC,先根据点A、C的坐标得到直线AC的解析式,再根据平行直线的解析式的k值相等求出过点B与AC平行的直线的解析式,然后与抛物线解析式联立求解即可得到点P的坐标;③BC是底边时,AP∥BC,根据点B、C的坐标求出直线BC的解析式,再根据平行直线的解析式的k值相等求出过点A与BC平行的直线的解析式,然后与抛物线解析式联立求解即可得到点P的坐标;
(4)△MBC的面积可由S△MBC=
| 1 |
| 2 |
解答: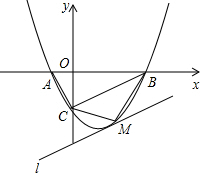 解:(1)将A(-1,0)、点C(0,-2).代入y=ax2-
解:(1)将A(-1,0)、点C(0,-2).代入y=ax2-
x+c(a≠0),得
,
解得
.
故该抛物线的解析式为:y=
x2-
x-2;
(2)由(1)的函数解析式可求得:B(4,0).
∵A(-1,0)、C(0,-2),
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,又:OC⊥AB,
∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
所以该外接圆的圆心为AB的中点,且坐标为:(
,0);
(3))①AB是底边时,PC∥AB,则点P的纵坐标与点C的纵坐标相同,是-2,
即
x2-
x-2=-2,
整理得,x2-3x=0,
解得x1=0(为点C坐标,舍去),x2=3,
所以,点P的坐标为(3,-2);
②AC是底边时,PB∥AC,由点A(-1,0)、C(0,-2)可得直线AC的解析式为y=-
x-2,
设直线PB的解析式为y=-
x+m,
把点B(4,0)代入得,-
×4+m=0,
解得m=2,
所以,直线PB的解析式为y=-
x+2,
则
,
解得
或
(为点B的坐标,舍去),
所以,点P的坐标为(-5,18);
③BC是底边时,AP∥BC,由点B(4,0)、C(0,-2)可得直线BC的解析式为y=2x-2,
设直线AP的解析式为y=2x+n,
把点A(-1,0)代入得,2×(-1)+n=0,
解得n=2,
所以,直线AP的解析式为y=2x+2,
则
,
解得
或
(为点A的坐标,舍去),
所以,点P的坐标为(5,3);
经检验,三种情况时,两底边都不相等,
综上所述,符合条件的点P共有3个:(3,-2)或(5,3)或(-5,18);
(4)已求得:B(4,0)、C(0,-2),可得直线BC的解析式为:y=
x-2;
设直线l∥BC,则该直线的解析式可表示为:y=
x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b=
x2-
x-2,即:
x2-2x-2-b=0,且△=0;
∴4-4×
(-2-b)=0,即b=-4;
∴直线l:y=
x-4.
∴点M即直线l和抛物线的唯一交点,则
,
解得:
,即 M(2,-3).
过M点作MN⊥x轴于N,
S△BMC=S梯形OCMN+S△MNB-S△OCB=
×2×(2+3)+
×2×3-
×2×4=4.
综上所述,点M(2,-3),△MBC面积最大值是4.
 解:(1)将A(-1,0)、点C(0,-2).代入y=ax2-
解:(1)将A(-1,0)、点C(0,-2).代入y=ax2-| 3 |
| 2 |
|
解得
|
故该抛物线的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)由(1)的函数解析式可求得:B(4,0).
∵A(-1,0)、C(0,-2),
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,又:OC⊥AB,
∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
所以该外接圆的圆心为AB的中点,且坐标为:(
| 3 |
| 2 |
(3))①AB是底边时,PC∥AB,则点P的纵坐标与点C的纵坐标相同,是-2,

即
| 1 |
| 2 |
| 3 |
| 2 |
整理得,x2-3x=0,
解得x1=0(为点C坐标,舍去),x2=3,
所以,点P的坐标为(3,-2);
②AC是底边时,PB∥AC,由点A(-1,0)、C(0,-2)可得直线AC的解析式为y=-
| 1 |
| 2 |
设直线PB的解析式为y=-
| 1 |
| 2 |
把点B(4,0)代入得,-
| 1 |
| 2 |
解得m=2,
所以,直线PB的解析式为y=-
| 1 |
| 2 |
则
|
解得
|
|
所以,点P的坐标为(-5,18);
③BC是底边时,AP∥BC,由点B(4,0)、C(0,-2)可得直线BC的解析式为y=2x-2,
设直线AP的解析式为y=2x+n,
把点A(-1,0)代入得,2×(-1)+n=0,
解得n=2,
所以,直线AP的解析式为y=2x+2,
则
|
解得
|
|
所以,点P的坐标为(5,3);
经检验,三种情况时,两底边都不相等,
综上所述,符合条件的点P共有3个:(3,-2)或(5,3)或(-5,18);
(4)已求得:B(4,0)、C(0,-2),可得直线BC的解析式为:y=
| 1 |
| 2 |
设直线l∥BC,则该直线的解析式可表示为:y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴4-4×
| 1 |
| 2 |
∴直线l:y=
| 1 |
| 2 |
∴点M即直线l和抛物线的唯一交点,则
|
解得:
|
过M点作MN⊥x轴于N,
S△BMC=S梯形OCMN+S△MNB-S△OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,点M(2,-3),△MBC面积最大值是4.
点评:考查了二次函数综合题,该题的难度不算太大,但用到的琐碎知识点较多,综合性很强.熟练掌握直角三角形的相关性质以及三角形的面积公式是理出思路的关键.(3)要分AB、AC、BC分别是底边三种情况讨论求解.

练习册系列答案
相关题目
 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )| A、70° | B、68° |
| C、60° | D、72° |
 已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点.
已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点. 如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据: 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下: 如图,直线y=ax+b与双曲线
如图,直线y=ax+b与双曲线