题目内容
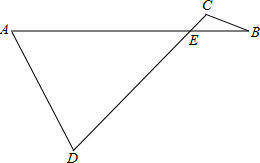 已知:AB、CD交于E点,连接AD、BC,
已知:AB、CD交于E点,连接AD、BC,(1)若AD+BC=3
| 2 |
| 2 |
(2)若∠B与∠D互为余角,∠A与∠C互为补角,则∠AEC的度数为
(3)在(1)(2)的条件下,若CD=4
| 2 |
考点:正弦定理与余弦定理,解二元一次方程组,解一元二次方程-因式分解法,三角形内角和定理,多边形内角与外角,平行四边形的性质
专题:计算题
分析:(1)根据条件建立方程组,即可解决问题.
(2)结合条件,利用三角形的内角和就可求出∠AED的度数,进而求出∠AEC的度数.
(3)以CD、CB为邻边作平行四边形BCDF,则有∠ABF=∠AED=45°,BF=DC=4
,在△ADF中运用余弦定理可求出AF2,再在△ABF中运用余弦定理就可求出AB.
(2)结合条件,利用三角形的内角和就可求出∠AED的度数,进而求出∠AEC的度数.
(3)以CD、CB为邻边作平行四边形BCDF,则有∠ABF=∠AED=45°,BF=DC=4
| 2 |
解答:解:(1)联立
,
解得:
.
故答案为:3
,1.
(2)如图1,
∵∠B与∠D互为余角,∠A与∠C互为补角,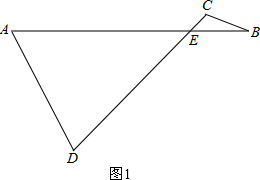
∴∠D+∠B=90°,∠A+∠C=180°.
∵∠A+∠D+∠AED=180°,
∠B+∠C+∠BEC=180°,
∴∠A+∠D+∠AED+∠B+∠C+∠BEC=360°.
∴∠AED+∠BEC+90°+180°=360°.
∴∠AED+∠BEC=90°.
∵∠AED=∠BEC,
∴∠AED=∠BEC=45°.
∴∠AEC=135°
故答案为:135°.
(3)以CD、CB为邻边作平行四边形BCDF,连接AF,如图2所示,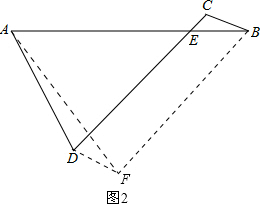
∵四边形BCDF是平行四边形,
∴BF=DC=4
,DF=BC=1,∠DFB=∠C=180°-∠DAB,DC∥BF.
∴∠ABF=∠AED=45°.
在四边形ABFD中,
∵∠DAB+∠ABF+∠BFD+∠ADF=360°,∠DFB=180°-∠DAB,∠ABF=45°,
∴∠ADF=135°.
在△ADF中,
∵AD=3
,DF=1,∠ADF=135°,
∴AF2=AD2+DF2-2AD•DF•cos∠ADF
=18+1-2×3
×1×(-
)
=25.
在△ABF中,
∵AF2=25,BF=4
,∠ABF=45°,
∴AF2=AB2+BF2-2AB•BF•cos∠ABF
=AB2+(4
)2-2×AB×4
×
=25.
解得:AB=1(舍去)或AB=7.
∴AB的长为7.
|
解得:
|
故答案为:3
| 2 |
(2)如图1,
∵∠B与∠D互为余角,∠A与∠C互为补角,

∴∠D+∠B=90°,∠A+∠C=180°.
∵∠A+∠D+∠AED=180°,
∠B+∠C+∠BEC=180°,
∴∠A+∠D+∠AED+∠B+∠C+∠BEC=360°.
∴∠AED+∠BEC+90°+180°=360°.
∴∠AED+∠BEC=90°.
∵∠AED=∠BEC,
∴∠AED=∠BEC=45°.
∴∠AEC=135°
故答案为:135°.
(3)以CD、CB为邻边作平行四边形BCDF,连接AF,如图2所示,

∵四边形BCDF是平行四边形,
∴BF=DC=4
| 2 |
∴∠ABF=∠AED=45°.
在四边形ABFD中,
∵∠DAB+∠ABF+∠BFD+∠ADF=360°,∠DFB=180°-∠DAB,∠ABF=45°,
∴∠ADF=135°.
在△ADF中,
∵AD=3
| 2 |
∴AF2=AD2+DF2-2AD•DF•cos∠ADF
=18+1-2×3
| 2 |
| ||
| 2 |
=25.
在△ABF中,
∵AF2=25,BF=4
| 2 |
∴AF2=AB2+BF2-2AB•BF•cos∠ABF
=AB2+(4
| 2 |
| 2 |
| ||
| 2 |
解得:AB=1(舍去)或AB=7.
∴AB的长为7.
点评:本题考查了余弦定理、解二元一次方程组、解一元二次方程、平行四边形的性质、三角形及四边形的内角和等知识,还考查了构造法,有一定的难度,而以CD、CB为邻边构造平行四边形是解决本题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 如图,直线y=ax+b与双曲线
如图,直线y=ax+b与双曲线 如图:在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2厘米/秒的速度移动,点Q沿DA边从D开始向点A以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图:在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2厘米/秒的速度移动,点Q沿DA边从D开始向点A以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).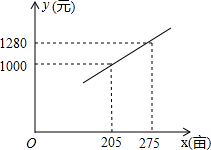 国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划明年再承租不超过90亩的土地种粮以增加收入,考虑各种因素,政府预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示:
国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划明年再承租不超过90亩的土地种粮以增加收入,考虑各种因素,政府预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示: