Question

1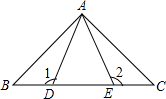．如图，AD=AE，BE=CD，∠1=∠2=120°，∠BAE=80°，那么∠CAE=20°．

Answer 1

分析 在△ABE中可求得∠B，则可求得∠BAD，由BE=CD可求得BD=CE，可证明△ABD≌△ACE，可求得∠CAE=∠BAD，可求得答案．

解答 解：
∵∠2=120°，∠BAE=80°，
∴∠B=∠2-∠BAE=120°-80°=40°，
∵BE=CD，
∴BD=CE，
在△ABD和△ACE中
$\left\{\begin{array}{l}{AD=AE}\\{∠1=∠2}\\{BD=CE}\end{array}\right.$
∴△ABD≌△ACE（SAS），
∴∠C=∠B=40°，
∴∠CAE=180°-∠2-∠C=180°-120°-40°=20°，
故答案为：20°．

点评 本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和全等三角形的性质（即对应边、对应角相等）是解题的关键．