题目内容
6. 如图,在△ABC中,BD是∠ABC的平分线,DE∥BC,BC=7,AE=4,求DE的长.
如图,在△ABC中,BD是∠ABC的平分线,DE∥BC,BC=7,AE=4,求DE的长.
分析 根据BD是∠ABC的平分线和DE∥BC得出∠2=∠3=∠1,即可知DE=BE,证△AED∽△ABC得$\frac{AE}{AB}=\frac{DE}{BC}$,即$\frac{4}{4+DE}=\frac{DE}{7}$,解之可得.
解答 解:如图,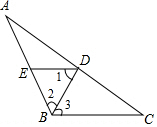
∵BD是∠ABC的平分线,
∴∠2=∠3,
∵DE∥BC,
∴∠1=∠3,
∴∠1=∠2,
∴DE=BE,
∵DE∥BC,
∴△AED∽△ABC,
∴$\frac{AE}{AB}=\frac{DE}{BC}$,即$\frac{4}{4+DE}=\frac{DE}{7}$,
解得:DE=-2+4$\sqrt{2}$或DE=-2-4$\sqrt{2}$(舍),
即DE的长为-2+4$\sqrt{2}$.
点评 此题考查了平行线的性质,相似三角形的判定与性质以及等腰三角形的判定与性质等知识.解题的关键是熟练掌握相似三角形的判定与性质.

练习册系列答案
相关题目
9.下列关系式正确的是( )
| A. | 35.5°=35°5′ | B. | 35.5°=35°50′ | C. | 35.5°>35°5′ | D. | 35.5°<35°5′ |
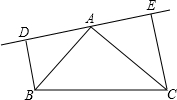 如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;若B,C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC.
如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;若B,C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC.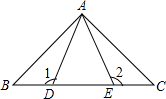 如图,AD=AE,BE=CD,∠1=∠2=120°,∠BAE=80°,那么∠CAE=20°.
如图,AD=AE,BE=CD,∠1=∠2=120°,∠BAE=80°,那么∠CAE=20°.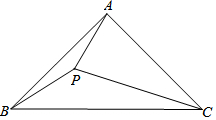 已知,如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P是△ABC内部一点,且PC=AC,∠PCA=120°-α.
已知,如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P是△ABC内部一点,且PC=AC,∠PCA=120°-α.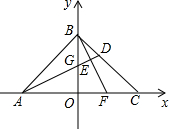 如图,在平面直角坐标系中,OA=OB=OC=6,点G的线段OB上的一个动点,连接AG并延长BC于点D.
如图,在平面直角坐标系中,OA=OB=OC=6,点G的线段OB上的一个动点,连接AG并延长BC于点D.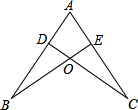 已知:点D在AB上,点E在AC上,BE和CD相交于点O,AD=AE,∠B=∠C. 求证:CD=BE.
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AD=AE,∠B=∠C. 求证:CD=BE.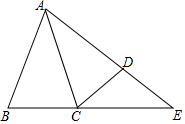 如图△ABC中,AB=AC=8,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD、BC交于点E,则DE的长是4$\sqrt{3}$-4.
如图△ABC中,AB=AC=8,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD、BC交于点E,则DE的长是4$\sqrt{3}$-4.