题目内容
 如图,一次函数y=-
如图,一次函数y=-| 3 |
| 3 |
(1)求A,B两点的坐标及线段AB的长.
(2)∠BAO=60°吗?说明理由;
(3)过AB为一边作等边三角形ABC,求点C的坐标.
考点:一次函数图象上点的坐标特征,等边三角形的性质
专题:
分析:(1)先令y=0求出x的值,再令x=0求出y的值即可得出A、B两点的坐标;
(2)根据A,B两点的坐标可得出OA与OB的长,由锐角三角函数的定义可得出∠BAO的度数;
(3)先根据勾股定理求出AB的长,再分点C在直线AB的右侧与左侧两种情况进行讨论.
(2)根据A,B两点的坐标可得出OA与OB的长,由锐角三角函数的定义可得出∠BAO的度数;
(3)先根据勾股定理求出AB的长,再分点C在直线AB的右侧与左侧两种情况进行讨论.
解答: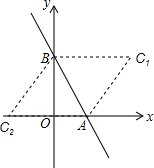 解;(1)∵令y=0,则x=1,令x=0,则y=
解;(1)∵令y=0,则x=1,令x=0,则y=
,
∴A(1,0),B(0,
);
(2)∠BAO=60°.
理由:∵由(1)知,A(1,0),B(0,
),
∴OA=1,OB=
,
∴tan∠BAO=
=
,
∴∠BAO=60°;
(3)∵由(2)知,OA=1,OB=
,
∴AB=
=2.
如图所示,
当点C在直线AB的右侧时,
∵∠BAO=60°,
∴∠OBA=30°.
∵△ABC1是等边三角形,
∴∠ABC1=60°,BC1=AB=2,
∴BC1∥OA,
∴C1(2,
);
当点C在直线AB的左侧时,
∵∠OBA=30°,
∴∠OBC2=30°,
∴OB是AC2的垂直平分线,
∴C2(-1,0).
综上所示,C点坐标为(2,
)或(-1,0).
 解;(1)∵令y=0,则x=1,令x=0,则y=
解;(1)∵令y=0,则x=1,令x=0,则y=| 3 |
∴A(1,0),B(0,
| 3 |
(2)∠BAO=60°.
理由:∵由(1)知,A(1,0),B(0,
| 3 |
∴OA=1,OB=
| 3 |
∴tan∠BAO=
| OB |
| OA |
| 3 |
∴∠BAO=60°;
(3)∵由(2)知,OA=1,OB=
| 3 |
∴AB=
12+(
|
如图所示,
当点C在直线AB的右侧时,
∵∠BAO=60°,
∴∠OBA=30°.
∵△ABC1是等边三角形,
∴∠ABC1=60°,BC1=AB=2,
∴BC1∥OA,
∴C1(2,
| 3 |
当点C在直线AB的左侧时,
∵∠OBA=30°,
∴∠OBC2=30°,
∴OB是AC2的垂直平分线,
∴C2(-1,0).
综上所示,C点坐标为(2,
| 3 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列说法错误的是( )
| A、三角形三条中线都能平分三角形的面积 |
| B、三角形三条角平分线交于三角形内一点 |
| C、三角形三条高交于一点 |
| D、三角形的中线、角平分线、高都是线段 |
 用30m篱笆围成三面是篱笆,一面用墙的矩形菜地.
用30m篱笆围成三面是篱笆,一面用墙的矩形菜地. 有一块两条直角边BC、AC的长分别为3厘米和4厘米的Rt△ABC的铁片,现要把它加工成一个面积尽最大的正方形,甲、乙两位师傅加工方案分别如图1和图2所示,请用你学过的知识说明哪位师傅的加工方案符合要求(加工中的损耗忽略不计).
有一块两条直角边BC、AC的长分别为3厘米和4厘米的Rt△ABC的铁片,现要把它加工成一个面积尽最大的正方形,甲、乙两位师傅加工方案分别如图1和图2所示,请用你学过的知识说明哪位师傅的加工方案符合要求(加工中的损耗忽略不计). 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC边于点E.若BE=2,∠B=22.5°
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC边于点E.若BE=2,∠B=22.5°