题目内容
3.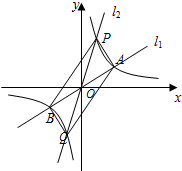 如图,经过原点的两条直线l1、l2分别与双曲线y=$\frac{k}{x}$(k≠0)相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
如图,经过原点的两条直线l1、l2分别与双曲线y=$\frac{k}{x}$(k≠0)相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).(1)求k值及B点坐标;
(2)若P点坐标为(a,3),求a值及四边形APBQ的面积.
分析 (1)根据分别反比例图象上点的坐标特征得到k=3×1=3,再根据正比例函数图象和反比例函数图象的性质得到点A与点B关于原点对称,则B点坐标为(-3,-1);
(2)先根据反比例函数图象上点的坐标特征得到a=1,即P点坐标为(1,3),再根据正比例函数图象和反比例函数图象的性质得到点P与点Q关于原点对称,所以点Q的坐标为(-1,-3),由于OA=OB,OP=OQ,则根据平行四边形的判定得到四边形APBQ为平行四边形,然后根据两点间的距离公式计算出AB,PQ,可得到即AB=PQ,于是可判断四边形APBQ为矩形,再计算出PA和PB,然后计算矩形APBQ的面积.
解答 解:(1)把A(3,1)代入=$\frac{k}{x}$得k=3×1=3,
∵经过原点的直线l1与双曲线=$\frac{k}{x}$(k≠0)相交于A、B、
∴点A与点B关于原点对称,
∴B点坐标为(-3,-1);
(2)把P(a,3)代入y=$\frac{3}{x}$得3a=3,解得a=1,
∵P点坐标为(1,3),
∵经过原点的直线l2与双曲线=$\frac{k}{x}$(k≠0)相交于P、Q点,
∴点P与点Q关于原点对称,
∴点Q的坐标为(-1,-3),
∵OA=OB,OP=OQ,
∴四边形APBQ为平行四边形,
∵AB2=(3+3)2+(1+1)2=40,PQ2=(1+1)2+(3+3)2=40,
∴AB=PQ,
∴四边形APBQ为矩形,
∵PB2=(1+3)2+(3+1)2=32,PQ2=(3-1)2+(1-3)2=8,
∴PB=4$\sqrt{2}$,PQ=2$\sqrt{2}$,
∴四边形APBQ的面积=PA•PB=2$\sqrt{2}$×4$\sqrt{2}$=16.
点评 本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、正比例函数图象与反比例函数图象的性质、中心对称的性质、矩形的性质;会利用两点间的距离公式计算线段的长.

| A. | 三条角平分线的交点 | B. | 三边垂直平分线的交点 | ||
| C. | 三条中线的交点 | D. | 三条高的交点 |
| A. | 互为倒数 | B. | 符号相同 | C. | 绝对值相等 | D. | 符号相反 |
| A. | 1<y<4 | B. | -4<y<-2 | C. | -4<y<-1 | D. | 2<y<4 |
 如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.
如图,四边形ABCD为正方形,P为正方形ABCD外一点△ABP经过旋转后到达△BCQ的位置,那么旋转中心是B,旋转角是90度.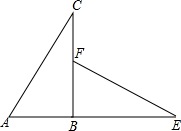 如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:
如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答: