题目内容
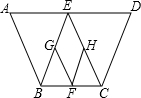 如图,等腰梯形ABCD中,AD∥BC,AB=CD,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.(1)当BE=CE时,求证:AE=DE;
(2)当点E运动到什么位置时,四边形EGFH是菱形?(直接写出结论即可,不用说明理由)
(3)若(2)中的菱形EGFH是正方形,线段EF与线段BC有什么关系?证明你的结论.
考点:等腰梯形的性质,菱形的判定与性质,正方形的性质
专题:
分析:(1)根据等腰梯形的性质得出∠A=∠D,∠ABC=∠DCB,根据BE=CE得出∠EBC=∠ECB,求出∠ABE=∠DCE,根据ASA推出△ABE≌△DCE即可;
(2)根据全等三角形的判定推出△ABE≌△DCE,求出BE=CE,根据三角形的中位线性质得出FG=
CE,FH=
BE,FG∥CE,FH∥BE,得出四边形EGFH是平行四边形,根据菱形的判定得出即可;
(3)根据正方形的性质得出∠BEC=90°,根据直角三角形的性质得出即可.
(2)根据全等三角形的判定推出△ABE≌△DCE,求出BE=CE,根据三角形的中位线性质得出FG=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据正方形的性质得出∠BEC=90°,根据直角三角形的性质得出即可.
解答:(1)证明:∵等腰梯形ABCD中,AD∥BC,AB=CD,
∴∠A=∠D,∠ABC=∠DCB,
∵BE=CE,
∴∠EBC=∠ECB,
∴∠ABC-∠EBC=∠DCB-∠ECB,
∴∠ABE=∠DCE,
在△ABE和△DCE中
∴△ABE≌△DCE,
∴AE=DE;
(2)解:点E运动到AD的中点时,四边形EGFH是菱形,
理由是:∵等腰梯形ABCD中,AD∥BC,AB=CD,
∴∠A=∠D,
∵E为AD的中点,
∴AE=DE,
在△ABE和△DCE中
∴△ABE≌△DCE,
∴BE=CE,
∵G、F、H分别是BE、BC、CE的中点,
∴FG=
CE,FH=
BE,FG∥CE,FH∥BE,
∴四边形EGFH是平行四边形,FG=FH,
∴四边形EGFH是菱形,
即点E运动到AD的中点时,四边形EGFH是菱形;
(3)EF=
BC,
证明:∵菱形EGFH是正方形,
∴∠BEC=90°,
∵F为BC的中点,
∴EF=
BC.
∴∠A=∠D,∠ABC=∠DCB,
∵BE=CE,
∴∠EBC=∠ECB,
∴∠ABC-∠EBC=∠DCB-∠ECB,
∴∠ABE=∠DCE,
在△ABE和△DCE中
|
∴△ABE≌△DCE,
∴AE=DE;
(2)解:点E运动到AD的中点时,四边形EGFH是菱形,
理由是:∵等腰梯形ABCD中,AD∥BC,AB=CD,
∴∠A=∠D,
∵E为AD的中点,
∴AE=DE,
在△ABE和△DCE中
|
∴△ABE≌△DCE,
∴BE=CE,
∵G、F、H分别是BE、BC、CE的中点,
∴FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EGFH是平行四边形,FG=FH,
∴四边形EGFH是菱形,
即点E运动到AD的中点时,四边形EGFH是菱形;
(3)EF=
| 1 |
| 2 |
证明:∵菱形EGFH是正方形,
∴∠BEC=90°,
∵F为BC的中点,
∴EF=
| 1 |
| 2 |
点评:本题考查了等腰梯形的性质,全等三角形的性质和判定,平行四边形的判定,菱形的判定,三角形的中位线性质,正方形的性质,直角三角形的性质的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,难度适中.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
在十二点三十分时,钟表上的时针与分针所成的角( )
| A、直角 | B、钝角 | C、平角 | D、锐角 |
我市某中学九年级一班准备组织参加旅游,班长把全班48名同学对旅游地点的意向绘制成了扇形统计图,其中“想去海洋馆学生数”的扇形圆心角为60°,则下列说法中正确的是( )
| A、想去海洋馆的学生占全班学生的60% | ||
| B、想去海洋馆学生有12人 | ||
| C、想去海洋馆的学生肯定最多 | ||
D、想去海洋馆学生占全班学生的
|
 画出下列几何体的三视图.
画出下列几何体的三视图.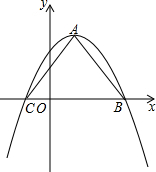 如图,在平面直角坐标系中,抛物线C1:y=-x2+2x+3的顶点为A,与x轴交于两点.
如图,在平面直角坐标系中,抛物线C1:y=-x2+2x+3的顶点为A,与x轴交于两点.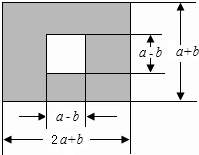 如图,某地有块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将搞一雕塑.
如图,某地有块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将搞一雕塑.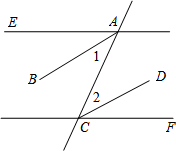 如图,直线AE、CF分别被直线AC所截,已知AE∥FC,AB平分∠EAC,CD平分∠ACF,将下列说明AB∥CD的过程及理由填写完整.
如图,直线AE、CF分别被直线AC所截,已知AE∥FC,AB平分∠EAC,CD平分∠ACF,将下列说明AB∥CD的过程及理由填写完整.