题目内容
17.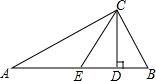 如图,在△ABC中,∠ACB=90°,CD、CE分别为斜边上的高、中线,那么:
如图,在△ABC中,∠ACB=90°,CD、CE分别为斜边上的高、中线,那么:(1)与CE相等的线段有AE、EB;
(2)与∠A度数相等的角有∠ACE;
(3)若∠A=35°,则∠ACE=35°,∠BCE=55°,∠CEB=70°,∠DCE=20°.
分析 (1)由直角三角形斜边上的中线等于斜边的一半进行解答;
(2)利用(1)中的相等线段和“等边对等角”进行解答;
(3)根据余角的定义,三角形内角和定理或者外角的性质进行答题即可.
解答  解:(1)∵在△ABC中,∠ACB=90°,CE为斜边上的中线,
解:(1)∵在△ABC中,∠ACB=90°,CE为斜边上的中线,
∴AE=CE=EB.
故答案是:AE、EB;
(2)由(1)知,AE=CE,则∠A=∠ACE.
故答案是:∠ACE;
(3)由(2)知,∠A=∠ACE.
∵∠A=35°,
∴∠ACE=35°.
∴∠CEB=∠A+∠ACE=70°
又∵∠ACB=90°,
∴∠B=55°.
∵EC=EB,
∴∠BCE=90°-∠ACE=55°.
又∵CD为斜边上的高,
∴∠DCE=180°-90°-35°-35°=20°.
故答案是:35°;55°;70°;20°.
点评 本题考查了三角形内角和定理,直角三角形斜边上的中线.解题时,注意“等边对等角”性质的应用和三角形内角和为180°的应用.

练习册系列答案
相关题目
8.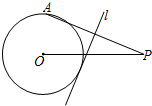 如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )
如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )
 如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )
如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )| A. | 10 | B. | $\frac{21}{2}$ | C. | 11 | D. | $\frac{43}{4}$ |
2.下列化简错误的是( )
| A. | $\sqrt{\frac{5}{12}}$=$\frac{\sqrt{15}}{6}$ | B. | $\sqrt{\frac{18}{5}}$=$\frac{3\sqrt{10}}{5}$ | C. | $\sqrt{\frac{7}{24}}$=$\frac{\sqrt{21}}{12}$ | D. | $\sqrt{\frac{3}{8}}$=$\frac{\sqrt{6}}{4}$ |
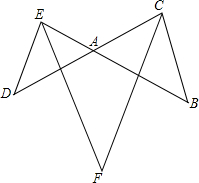 已知如图所示,E和D分别是△ABC边CA、BA延长线上一点,EF、CF分别平分∠AED、∠ACB.若∠B=70°,∠D=40°,求∠F的度数.
已知如图所示,E和D分别是△ABC边CA、BA延长线上一点,EF、CF分别平分∠AED、∠ACB.若∠B=70°,∠D=40°,求∠F的度数. 如图,将△ABC沿BC方向平移线段$\frac{1}{2}$BC的长度得到△DEF,点A与点D对应,点B与点E对应,画出平移后的图形并回答下列问题:
如图,将△ABC沿BC方向平移线段$\frac{1}{2}$BC的长度得到△DEF,点A与点D对应,点B与点E对应,画出平移后的图形并回答下列问题: 有理数a,b在数轴上对应的位置如图所示,试化简|a-b|-|a|+|b|.
有理数a,b在数轴上对应的位置如图所示,试化简|a-b|-|a|+|b|.