题目内容
19.观察下列式子:1=2×$\frac{0}{1}$+1,2=3×$\frac{1}{2}$+$\frac{1}{2}$,3=4×$\frac{2}{3}$+$\frac{1}{3}$,4=5×$\frac{3}{4}$+$\frac{1}{4}$…
根据上述规律,请猜想,若n为正整数,则n=(n+1)×$\frac{n-1}{n}$+$\frac{1}{n}$.
分析 由1=2×$\frac{0}{1}$+1,2=3×$\frac{1}{2}$+$\frac{1}{2}$,3=4×$\frac{2}{3}$+$\frac{1}{3}$,4=5×$\frac{3}{4}$+$\frac{1}{4}$…得出第n个式子为n=(n+1)×$\frac{n-1}{n}$+$\frac{1}{n}$,由此得出答案即可.
解答 解:∵1=2×$\frac{0}{1}$+1,
2=3×$\frac{1}{2}$+$\frac{1}{2}$,
3=4×$\frac{2}{3}$+$\frac{1}{3}$,
4=5×$\frac{3}{4}$+$\frac{1}{4}$,
…
∴第n个式子为n=(n+1)×$\frac{n-1}{n}$+$\frac{1}{n}$.
故答案为:(n+1)×$\frac{n-1}{n}$+$\frac{1}{n}$.
点评 此题考查数字的变化规律,找出运算中数字的变化特点,得出运算的规律解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知x=1是方程x2+x-2a=0的一个根,则方程的另一个根是( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
14.从下列4个命题中任取一个 ①6的平方根是$\sqrt{6}$; ②$\sqrt{6}$是方程x2-6=0的解; ③如果两个图形是位似图形,则这两个图形一定相似.④在半径为4的圆中,15°的圆周角所对的弧长为$\frac{2}{3}$π;是真命题的概率是( )
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
4.已知关于的方程x2+2(1+a)x+(3a2+4ab+4b2+2)=0有实数根.已知点A(a,y1),B(b,y2)都在一次函数y=kx(k>0)的图象上,则y1-y2的值为( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
8.如图,是2015年杭州市某月24日08时至25日07时的空气质量指数统计图(空气质量指数AQI的值在不同的区间,就代表了不同的空气质量水平.比如0-50之间,代表“良好”,对应的颜色为绿色;51-100之间,代表“中等”,对应的颜色为黄色;101-150之间,代表“对敏感人群不健康”,对应的颜色为橙色等等.),则根据统计图得出的下列判断,正确的是( )
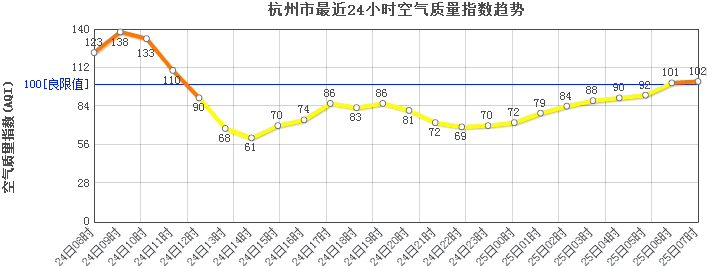

| A. | 在这个24小时中,AQI的值超过良限值时段是24日08时至24日12时 | |
| B. | 在这个24小时中,AQI对应的颜色为黄色的时段持续了20小时以上 | |
| C. | 在这个24小时中,AQI的最大值和最小值的差为77 | |
| D. | 建议中老年朋友在25日06时至07时进行晨练 |