题目内容
4.已知关于的方程x2+2(1+a)x+(3a2+4ab+4b2+2)=0有实数根.已知点A(a,y1),B(b,y2)都在一次函数y=kx(k>0)的图象上,则y1-y2的值为( )| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
分析 先根据题意得出a,b的值,再判断出函数的增减性,根据a,b的大小即可得出结论.
解答 解:∵关于的方程x2+2(1+a)x+(3a2+4ab+4b2+2)=0有实数根,
∴△≥0,即[2(1+a)]2-4(3a2+4ab+4b2+2)≥0,
∴(a+2b)2+(a-1)2≤0 ①
∵(a+2b)2≥0且(a-1)2≥0,得(a+2b)2+(a-1)2≥0 ②
∴只有当(a+2b)2=0且(a-1)2=0不等式①和②才能同时成立.
∴a=1,b=-$\frac{1}{2}$.
∵一次函数y=kx中k>0,
∴y随x的增大而增大,
∵1>-$\frac{1}{2}$,
∴y1>y2,
∴y1-y2>0.
故选A.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
9.下列命题中是假命题的是( )
| A. | 垂直于弦的直径平分弦 | |
| B. | 若a>b,c>0,则ac>bc | |
| C. | 反比例函数y=$\frac{k}{x}$,当k>0时,y随x的增大而减少 | |
| D. | 对角线互相平分且垂直的四边形是菱形 |
16.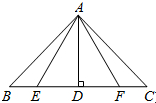 如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
 如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
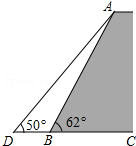 如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20) 正整数如图的规则排列,则:
正整数如图的规则排列,则:
 已知:如图,D是△ABC边BC上一点,且∠B=∠1,求证:∠2=∠BAC.
已知:如图,D是△ABC边BC上一点,且∠B=∠1,求证:∠2=∠BAC.