题目内容
9.(1)计算:($\frac{1}{2}$)-1+$\sqrt{12}$-4sin60°-|$\sqrt{3}$-2|(2)先化简,再求值:$\frac{{x}^{2}-1}{{x}^{2}-x}$÷(2+$\frac{{x}^{2}+1}{x}$),其中x=$\sqrt{2}$-1.
分析 (1)原式第一项利用负指数幂法则计算,第二项化为最简二次根式,第三项利用特殊角的三角函数值计算,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:(1)原式=2+2$\sqrt{3}$-4×$\frac{\sqrt{3}}{2}$-2+$\sqrt{3}$=$\sqrt{3}$;
(2)原式=$\frac{(x+1)(x-1)}{x(x-1)}$÷$\frac{2x+{x}^{2}+1}{x}$=$\frac{(x+1)(x-1)}{x(x-1)}$•$\frac{x}{(x+1)^{2}}$=$\frac{1}{x+1}$,
当x=$\sqrt{3}$-1时,原式=$\frac{1}{\sqrt{2}-1+1}$=$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | 2a6÷a3=2a2 | C. | -5a+4a=-1 | D. | 3a•(-2a)2=12a3 |
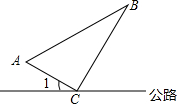 如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?
如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?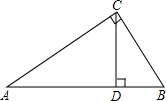 △ABC中,∠C=90°,BC=3,AB=5,CD⊥AB于D,
△ABC中,∠C=90°,BC=3,AB=5,CD⊥AB于D,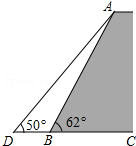 如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)