题目内容
7.先化简,再求值($\frac{1}{x}$-$\frac{2}{x-1}$)÷$\frac{1}{{x}^{2}-x}$,其中x满足不等式组$\left\{\begin{array}{l}{x+1<3}\\{2x+9>3}\end{array}\right.$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出不等式组的解集确定出x的值,代入计算即可求出值.
解答 解:原式=[$\frac{x-1}{x(x-1)}$-$\frac{2x}{x(x-1)}$]•x(x-1)=$\frac{x-1-2x}{x(x-1)}$•x(x-1)=-x-1,
解不等式组$\left\{\begin{array}{l}{x+1<3①}\\{2x+9>3②}\end{array}\right.$,
由①得x<2;
由②得x>-3,
∴-3<x<2,
当x=-1时,原式=0.
点评 此题考查了分式的化简求值,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | 2a6÷a3=2a2 | C. | -5a+4a=-1 | D. | 3a•(-2a)2=12a3 |
2.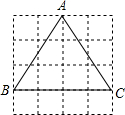 正方形网格中,△ABC如图放置,则sin∠BAC=( )
正方形网格中,△ABC如图放置,则sin∠BAC=( )
 正方形网格中,△ABC如图放置,则sin∠BAC=( )
正方形网格中,△ABC如图放置,则sin∠BAC=( )| A. | $\frac{2}{{\sqrt{13}}}$ | B. | $\frac{3}{{\sqrt{13}}}$ | C. | $\frac{4}{{\sqrt{13}}}$ | D. | $\frac{12}{13}$ |
16.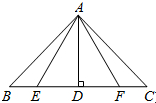 如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
 如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
 正整数如图的规则排列,则:
正整数如图的规则排列,则: