题目内容
19.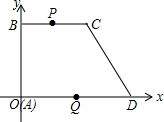 如图,在平面直角坐标系中,梯形ABCD的坐标为A(0,0),B(0,8),C(8,8),D(12,0).点P,Q分别从B,D出发以1个单位/秒和2个单位/秒的速度向C,O运动,设运动时间为t(s)(一点到达,另一点也停止运动).
如图,在平面直角坐标系中,梯形ABCD的坐标为A(0,0),B(0,8),C(8,8),D(12,0).点P,Q分别从B,D出发以1个单位/秒和2个单位/秒的速度向C,O运动,设运动时间为t(s)(一点到达,另一点也停止运动).(1)写出线段CD的中点坐标(10,4),梯形面积为80;
(2)t为何值时,四边形BPQA为长方形?
分析 (1)作CM⊥AD于M,取CD的中点E,作EN⊥AD于N,则CM∥EN,由点的坐标得出OM=BC=8,CM=8,DM=4,MN=DN=2,EN=$\frac{1}{2}$CM=4,再利用梯形面积公式求出面积即可;
(2)由题意得出BP=AQ,得出方程,解方程即可.
解答 解:(1)作CM⊥AD于M,取CD的中点E,作EN⊥AD于N,如图所示:
则CM∥EN,
∵梯形ABCD的坐标为:A(0,0),B(0,8),C(8,8),D(12,0),
∴OM=BC=8,CM=8,DM=12-8=4,MN=DN=2,EN=$\frac{1}{2}$CM=4,
∴ON=8+2=10,
∴线段CD的中点坐标为:(10,4),
梯形面积=$\frac{1}{2}$(BC+OD)×BO=$\frac{1}{2}$(8+12)×8=80;
故答案为:(10,4),80;
(2)若四边形BPQA为长方形,则BP=AQ,
∴t=12-2t,
解得:t=4.
即t=4时,四边形BPQA为长方形.
点评 此题主要考查了梯形的性质、长方形的性质和坐标与图形性质等知识;由平行四边形得出BP=AQ是解决问题(2)的关键.

练习册系列答案
相关题目
9.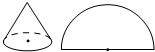 如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是( )
如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是( )
 如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是( )
如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
8.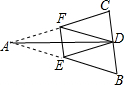 如图,在△ABC中,AB=AC,点D为BC边的中点,将△ABC沿EF折叠,点A与点D重合,若DE=$\sqrt{10}$,EF=2,则△ABC的面积为( )
如图,在△ABC中,AB=AC,点D为BC边的中点,将△ABC沿EF折叠,点A与点D重合,若DE=$\sqrt{10}$,EF=2,则△ABC的面积为( )
 如图,在△ABC中,AB=AC,点D为BC边的中点,将△ABC沿EF折叠,点A与点D重合,若DE=$\sqrt{10}$,EF=2,则△ABC的面积为( )
如图,在△ABC中,AB=AC,点D为BC边的中点,将△ABC沿EF折叠,点A与点D重合,若DE=$\sqrt{10}$,EF=2,则△ABC的面积为( )| A. | 2$\sqrt{10}$ | B. | 4$\sqrt{10}$ | C. | 12 | D. | 24 |
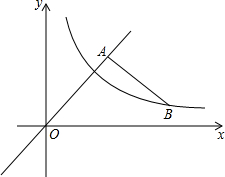 如图,已知A为直线y=x上一点,过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B,若OA2-AB2=8,求k的值.
如图,已知A为直线y=x上一点,过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B,若OA2-AB2=8,求k的值.