题目内容
 如图,AC∥BD∥EF,AC=20,BD=80,则EF=
如图,AC∥BD∥EF,AC=20,BD=80,则EF=考点:相似三角形的判定与性质
专题:
分析:根据相似三角形的判定与性质,可得AE:ED的值,根据线段的和差,可用AE表示AD,再根据相似三角形对应边的比相等,可得EF:BD的值,可得答案.
解答:解:∵AC∥BD∥EF,
∴△ACE∽△DBE,
∴
=
=
,ED=4AE,
AD=AE+ED=5AE,
∵BD∥EF,
∴
=
=
=
,
∵BD=80,
∴EF=
×80=16,
故答案为:16.
∴△ACE∽△DBE,
∴
| AE |
| ED |
| AC |
| BD |
| 1 |
| 4 |
AD=AE+ED=5AE,
∵BD∥EF,
∴
| EF |
| BD |
| AE |
| AD |
| AE |
| 5AE |
| 1 |
| 5 |
∵BD=80,
∴EF=
| 1 |
| 5 |
故答案为:16.
点评:本题考查了相似三角形的判定与性质,利用了平行于三角形一边且与其它两边相交所得的三角形与原三角形相似,又利用了相似三角形对应边的比相等.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
下列各组代数式中,属于同类项的是( )
A、
| ||||
| B、m2n和m2p | ||||
| C、5p3q和-2p3q | ||||
| D、3x和3y |
经专家估算,南海内的油气资源约合15000亿美元,用科学记数法表示数字15000是( )
| A、15×103 |
| B、1.5×104 |
| C、1.5×103 |
| D、1.5×105 |
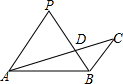 如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )
如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )| A、16 | B、15 | C、7 | D、6 |
一物体及其主视图如图所示,则它的左视图与俯视图分别是图形中的( )


| A、①② | B、③② | C、①④ | D、③④ |
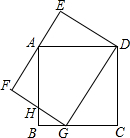 如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.
如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.