题目内容
20.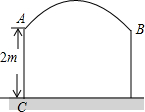 某村想在村口建一个如图形状的牌门,已知弧$\widehat{AB}$是所在圆的三分之一圆,立柱AC高2m,若要使高3m,宽2m的集装箱货车能通过,问AB的半径应大于多少m?
某村想在村口建一个如图形状的牌门,已知弧$\widehat{AB}$是所在圆的三分之一圆,立柱AC高2m,若要使高3m,宽2m的集装箱货车能通过,问AB的半径应大于多少m?
分析 设货车顶部为MN,要使货车刚好能通过,则M、N在AB弧上,且MN∥AB,MN=2m,MN离地面高度为3m,设圆心为点O,圆的半径为x,连接OA、OM,作OF垂直AB,交圆于F,交AB于E,交MN于G,根据勾股定理得到OM2=OG2+MG2,即可求出AB的半径.
解答 解:设货车顶部为MN,要使货车刚好能通过,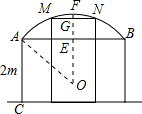
则M、N在AB弧上,且MN∥AB,MN=2m,MN离地面高度为3m,
设圆心为点O,圆的半径为x,连接OA、OM,作OF垂直AB,交圆于F,交AB于E,交MN于G,
则OF⊥MN,GE=3-2=1(m),
根据垂径定理知:MG=NG=1m,
$\widehat{AF}$=$\widehat{BF}$,
∵弧$\widehat{AB}$是所在圆的三分之一圆,
∴弧AF的度数=60°,
∴∠AOF=60°,∠OAE=30°,
∴OE=$\frac{OA}{2}$=$\frac{x}{2}$,
在直角三角形OMG中,根据勾股定理得:
OM2=OG2+MG2,
所以x2=1+($\frac{x}{2}$+1)2,
整理得:3x2-4x-8=0,
解得:x=$\frac{2±2\sqrt{7}}{3}$,
舍去负值得半径为$\frac{2+2\sqrt{7}}{3}$(m),
则弧AB的半径应大于$\frac{2+2\sqrt{7}}{3}$m
点评 本题考查了垂径定理的应用,与勾股定理相结合是解题的关键,要善于把实际问题与数学中的理论知识联系起来,能将生活中的问题抽象为数学问题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
5.一个多边形,它的每个内角都等于相邻外角的5倍,则这个多边形是( )
| A. | 正五边形 | B. | 正十边形 | C. | 正十二边形 | D. | 不存在 |
 如图,小球的质量x的取值范围是2<x<5.
如图,小球的质量x的取值范围是2<x<5.