Question

14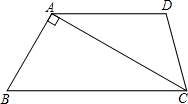．如图，在梯形ABCD中，AD∥BC，∠B=60°，∠ADC=105°，AD=6，且AC⊥AB，求AC的长．

Answer 1

分析 首先过点D作DE⊥AC于点E，并延长交BC于点F，易得四边形ABCD是平行四边形，即可求得∠ADE=60°，∠CDE=45°，又由AD=6，即可求得AE，CE的长，继而求得答案．

解答 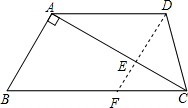解：过点D作DE⊥AC于点E，并延长交BC于点F，
∵AC⊥AB，
∴DE∥AB，
∵AD∥BC，
∴四边形ABCD是平行四边形，
∴∠ADF=∠B=60°，
∴AE=AD•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$，DE=$\frac{1}{2}$AD=3，
∵∠ADC=105°，
∴∠CDE=∠ADC-∠ADE=45°，
∴CE=DE=3，
∴AC=AE+CE=$3\sqrt{3}+3$．

点评 此题考查了梯形的性质、平行四边形的判定与性质以及三角函数等知识．注意准确作出辅助线是解此题的关键．