Question

15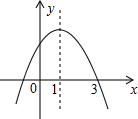．已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，现有下列结论：
①abc＞0；②b²-4ac＜0；③2a+b=0；④a+b＞0．
则其中正确结论的个数是（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 首先根据开口方向确定a的取值范围，根据对称轴的位置确定b的取值范围，根据抛物线与y轴的交点确定c的取值范围，根据抛物线与x轴是否有交点确定b²-4ac的取值范围，根据对称轴x=-$\frac{b}{2a}$=1即可确定2a+b的取值范围，根据b=-2a，a＜0可以确定a+b＞0是否成立．

解答 解：∵抛物线开口朝下，
∴a＜0，
∵对称轴x=1=-$\frac{b}{2a}$，
∴b＞0，
∵抛物线与y轴的交点在x轴的上方，
∴c＞0，
∴abc＜0，故①错误；
根据图象知道抛物线与x轴有两个交点，
∴b²-4ac＞0，故②错误．
∵对称轴x=-$\frac{b}{2a}$=1，
∴b=-2a，
∴2a+b=0，故③正确；
∵b=-2a，
∴a+b=a-2a=-a，
∴a＜0，
∴-a＞0，
∴a+b＞0，故④正确；
故选B．

点评 此题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．