题目内容
12.已知过点(1,-1)的直线y=kx+b(k≠0)不经过第一象限,设m=k2-$\frac{2}{3}$b,则m的取值范围是$\frac{5}{9}$≤m≤1.分析 先利用一次函数图象上点的坐标特征得到b=-k-1,再利用一次函数与系数的关系得到k<0,b≤0,则k的范围为-1≤k<0,接着用k表示m,然后根据二次函数的性质求m的范围.
解答 解:把(1,-1)代入y=kx+b得k+b=-1,b=-k-1,
因为直线y=kx+b(k≠0)不经过第一象限,
所以k<0,b≤0,即-k-1≤0,
所以k的范围为-1≤k<0,
因为m=k2-$\frac{2}{3}$b=k2-$\frac{2}{3}$(-k-1)=k2+$\frac{2}{3}$k+$\frac{2}{3}$=(k+$\frac{1}{3}$)2+$\frac{5}{9}$,
k<-$\frac{1}{3}$,m随k的增大而减小,
所以当k=-$\frac{1}{3}$时,m有最小值,最小值为$\frac{5}{9}$;k=-1时,m有最大值,最大值为(-1+$\frac{1}{3}$)2+$\frac{5}{9}$=1,
所以m的范围为$\frac{5}{9}$≤m≤$\frac{7}{3}$.
故答案为$\frac{5}{9}$≤m≤1.
点评 本题考查了一次函数与系数的关系:对于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴;当k>0,b>0?y=kx+b的图象在一、二、三象限;k>0,b<0?y=kx+b的图象在一、三、四象限;k<0,b>0?y=kx+b的图象在一、二、四象限;k<0,b<0?y=kx+b的图象在二、三、四象限.解决本题的关键是用k表示出m.

练习册系列答案
相关题目
 如图,OA=2,OB=3,将△AOB绕点A旋转,得△ADE,当点D落在AB上时,求点D的坐标.
如图,OA=2,OB=3,将△AOB绕点A旋转,得△ADE,当点D落在AB上时,求点D的坐标.
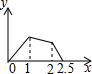
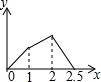
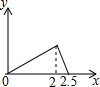
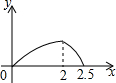
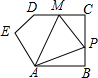 在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )
在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )