题目内容
16.计算:(1)${({-\frac{1}{2}})^2}÷{({-2})^{-3}}+{2^{-2}}×{(-3)^0}$
(2)(a+2)(a-2)-a(a-1)
(3)(-2a2b3)4+(-a8)•(2b4)3
(4)(2x+y-3)(2x-y-3)
分析 (1)根据幂的乘方、负整数指数幂、零指数幂可以解答本题;
(2)根据平方差公式、单项式乘以多项式可以解答本题;
(3)根据积的乘方,然后合并同类项即可解答本题;
(4)根据平方差公式和完全平方公式可以解答本题.
解答 解:原式=$\frac{1}{4}÷({-\frac{1}{8}})+\frac{1}{4}×1$
=$\frac{1}{4}×(-8)+\frac{1}{4}$
=-2+$\frac{1}{4}$
=-1$\frac{3}{4}$;
(2)原式=a2-4-a2+a
=a-4;
(3)原式=16a8b12+(-a8)•(8b12)
=16a8b12-8a8b12
=8a8b12;
(4)原式=[(2x-3)+y][(2x-3)-y]
=(2x-3)2-y2
=4x2-12x+9-y2.
点评 本题考查零指数幂、负整数指数幂、整式的混合运算、平方差公式、完全平方公式,解题的关键是明确它们各自的计算方法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
11. 如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
 如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |

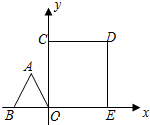 如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是11-2$\sqrt{3}$.
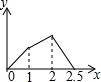
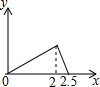
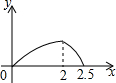
如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是11-2$\sqrt{3}$.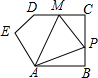 在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )
在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )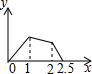
 将一副三角板按如图方式进行摆放,请判断∠1,∠2是否互补,并说明理由.
将一副三角板按如图方式进行摆放,请判断∠1,∠2是否互补,并说明理由.