题目内容
已知当x=1时，2ax2+bx的值为-2，求当x=2时，ax2+bx的值．
考点：代数式求值
专题：整体思想
分析：把x=1代入代数式求出a、b的关系式，再把x=2代入代数式整理即可得解．
解答：解：将x=1代入2ax2+bx=-2中，
得2a+b=-2，
当x=2时，ax2+bx=4a+2b，
=2（2a+b），
=2×（-2），
=-4．
得2a+b=-2，
当x=2时，ax2+bx=4a+2b，
=2（2a+b），
=2×（-2），
=-4．
点评：本题考查了代数式求值，整体思想的利用是解题的关键．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
如图，函数y=kx（k≠0）和y=ax+4（a≠0）的图象相交于点A（2，3），则不等式kx＞ax+4的解集为（ ）| A、x＞3 | B、x＜3 |
| C、x＞2 | D、x＜2 |
若a＞b，则下列不等式中，不成立的是（ ）
| A、a+5＞b+5 |
| B、a-5＞b-5 |
| C、5a＞5b |
| D、-5a＞-5b |
下列函数中，是一次函数但不是正比例函数的为（ ）
A、y=-
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
如图，在梯形AOBC中，AO∥CB，点A、B分别在y轴和x轴上．P是OB中点，以P为圆心，PB长为半径作半圆，D为该半圆与AC的一个公共点，且OB=CB=CD=4．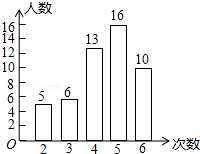
我市开展了“寻找雷锋足迹”的活动，某中学为了了解七年在“学雷锋活动月”中做好事的情况，随机调查了七年级50名学生在一个月内做好事的次数，并将所得数据绘制成统计图，请根据图中提供的信息解答下列问题：