题目内容
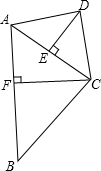 如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.
如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.(1)求AD的长;
(2)若DE⊥AC,CF⊥AB,垂足分别为E、F,求DE、CF的值.
考点:勾股定理
专题:
分析:(1)利用相似三角形的判定及其性质即可解决问题.
(2)利用勾股定理及三角形的面积公式即可解决问题.
(2)利用勾股定理及三角形的面积公式即可解决问题.
解答: 解:(1)∵AC平分∠BAD,BC⊥AC,CD⊥AD,
解:(1)∵AC平分∠BAD,BC⊥AC,CD⊥AD,
∴∠BAC=∠CAD,∠BCA=∠CDA,
∴△ABC∽△ACD,
∴
=
,AD=
=
=8,
即AD的长为8.
(2)由勾股定理得:DC=
=
=
=4
,
∵AD⊥DC,DE⊥AC,∴
AD•DC=
AC•DE,
∴DE=
=
;
∵AC平分∠BAD,CD⊥AD,CF⊥AB,
∴CF=CD=4
;
即DE、CF的值分别为
,4
.
 解:(1)∵AC平分∠BAD,BC⊥AC,CD⊥AD,
解:(1)∵AC平分∠BAD,BC⊥AC,CD⊥AD,∴∠BAC=∠CAD,∠BCA=∠CDA,
∴△ABC∽△ACD,
∴
| AB |
| AC |
| AC |
| AD |
| AC2 |
| AB |
| 122 |
| 18 |
即AD的长为8.
(2)由勾股定理得:DC=
| AC2-AD2 |
| 122-82 |
| 20×4 |
| 5 |
∵AD⊥DC,DE⊥AC,∴
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=
8×4
| ||
| 12 |
8
| ||
| 3 |
∵AC平分∠BAD,CD⊥AD,CF⊥AB,
∴CF=CD=4
| 5 |
即DE、CF的值分别为
8
| ||
| 3 |
| 5 |
点评:该题主要考查了勾股定理及其应用问题;同时还渗透了对相似三角形的判定及其性质的考查;对综合分析问题解决问题的能力提出了较高要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC中,∠BAC=54°,∠BAC的外角平分线交直线BC于D,若AB+AC=BD,求∠ABC的度数.
如图,△ABC中,∠BAC=54°,∠BAC的外角平分线交直线BC于D,若AB+AC=BD,求∠ABC的度数.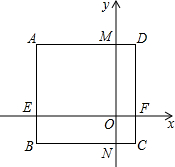 长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(-1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.
长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(-1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.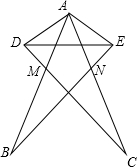 支撑高压电线的铁塔如图,其中AM=AN,∠DAB=∠EAC,AB=AC,问AD与AE能相等吗?为什么?
支撑高压电线的铁塔如图,其中AM=AN,∠DAB=∠EAC,AB=AC,问AD与AE能相等吗?为什么?